There are several items of news worth mentioning.
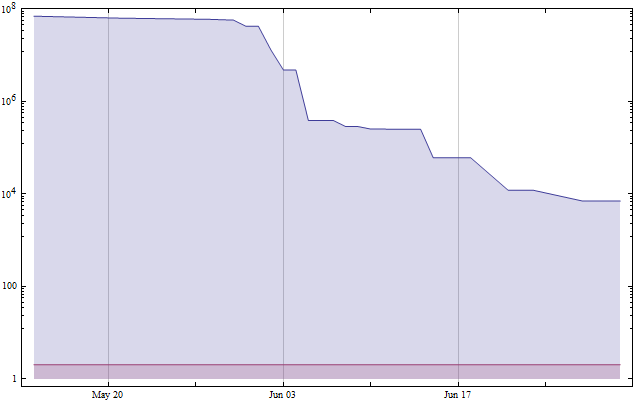
Firstly, I have been informed that the current status of the ‘bounded gaps between primes’ effort has now reached H = 6966, which is impressively low for these sieve methods. According to the status page, this is still an unconfirmed result. If we plot the results on a logarithmic plot, there appears to be an exponential decay.
Unfortunately, this trend is unlikely to continue, as major theoretical breakthroughs would be required in order to prove the twin prime conjecture (corresponding to the horizontal red line at H = 2).
Speaking of records, this year’s Senior Wrangler, Arran Fernandez, is suspected to be the youngest in history, winning Part II of the Mathematical Tripos at the age of just eighteen. Also, he is almost certainly the first Senior Wrangler from his college, Fitzwilliam.
Neither the collaborative ‘bounded gaps between primes’ project nor the Mathematical Tripos are actually competitions, but the same cannot be said of the 2013 Balkan Mathematical Olympiad, which is occurring in Agros, Cyprus at the moment. One of the contestants sent in a picture of an icosahedral Tarsia puzzle:
This is a welcome change from the more familiar planar variants. Continuing this sequence of smooth segues, the most common way to turn a dodecahedron into an icosahedron (or vice-versa) is by projective duality. There is a more incremental process, however, which consists of applying eight successive wye-delta transforms. If we insist that they occur in antipodal pairs to maintain central symmetry, a total of seven polyhedra can be formed, of which two are the dodecahedron and icosahedron. These polyhedra are double covers of the Petersen family of graphs, depicted in the following diagram by David Eppstein:

In the diagram, rotation by 180° corresponds to taking the projective dual of the corresponding polyhedron. In the middle of the diagram is the graph of the projectivisation of a centrally symmetric self-dual polyhedron, which can be regarded as precisely halfway between the icosahedron and dodecahedron.
Other polyhedra in this family include the hexakis hexagonal prism and its dual.


I think Part IB is the second year, whereas Senior Wrangler applies to Part II, the third year.
Yes, you’re absolutely correct, of course. I was somewhat distracted when I typed that, and it has since been amended.
And, whilst I’m at it, I’ve corrected ‘Argos’ to ‘Agros’ as the location of the Balkan Mathematical Olympiad. I don’t think that the chain of catalogue-based retail outlets would be particularly conducive to competitive problem-solving.
This year’s Senior Wrangler is probably not just the first from Fitzwilliam College, but the first from any of the ‘new’ colleges, defined as those founded in or after 1800 (or equivalently, 1597).
(The 1959 Senior Wrangler, Jayant Narlikar, was non-collegiate.)