A particularly important function is Klein’s j-function. It is defined on the upper half-plane of the complex numbers, and is incredibly symmetrical. For example, it is periodic, and thus invariant under translations by integers:

It is also invariant under a larger group of Möbius transformations, namely those corresponding to matrices with integer entries. This group is called the modular group, or , since it is the special linear group of invertible matrices with integer entries, quotiented out by its centre of order 2.
We can think of the upper half-plane as Klein’s model of the hyperbolic plane, in which case the j-function is a function on the hyperbolic plane and the Möbius transformations correspond to orientation-preserving isometries. Hence, an equivalent definition of the modular group is the orientation-preserving symmetry group of a regular tiling of the hyperbolic plane: the Voronoi tessellation of the zeros of the j-function.
Recall that the group of proper orthochronous Lorentz transformations is isomorphic to . Consequently, we can think of the modular group as a discrete version of this.
Fundamental groups and the complement of the trefoil knot
A surprising isomorphism pertains to knot theory and homotopy. Let X be a path-connected topological space. Then, we consider closed paths in X, beginning and ending at some pre-specified point. Under concatenation of paths, these form a monoid. When we quotient out by the relation ‘two paths are equivalent if they can be continuously deformed into each other’, then we get the fundamental group of X.
The fundamental group of any simply-connected space is just the trivial group, as any two paths can be continuously deformed into each other. The once-punctured plane has the infinite cyclic group as its fundamental group, since a path is determined up to continuous deformation by the number of times it encircles the puncture. The fundamental group of the twice-punctured plane is the free group on two generators, best visualised by its Cayley graph:
Now embed the trefoil knot in and consider its complement. It is a remarkable fact that the fundamental group of the resulting space, when quotiented by its centre, yields a group isomorphic to the modular group!

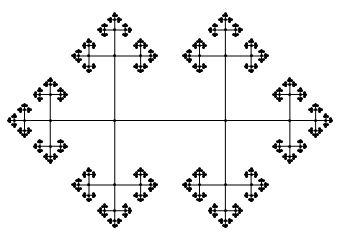
that’s not the free group on two generators…
What isn’t the free group on two generators? The fundamental group of the twice-punctured plane or [the group corresponding to] that Cayley graph? I’m pretty sure they are both the free group on two generators.
The cayley graph you have isn’t the free group on two generators.
There’s only one 4-regular tree, and this is it…