Let P(x) be a polynomial of degree n. Let H(i) represent the number of `1’s in the binary expansion of the integer i. Although reasonably easy to prove, it may seem surprising that the following identity holds:
Does this theorem have a name? I discovered a variation of it years ago when solving a problem given to me by James Aaronson, and applied it again this weekend to reduce an infinite problem to a finite one. One nice corollary of this theorem is that any arithmetic progression of 
- A and B contain equally many elements;
- The sums of the elements of A and B are equal;
- The sums of squares of elements of A and B are equal;
- (ellipsis)
- The sums of the nth powers of elements of A and B are equal.
By iterative application of this theorem, we can partition an arithmetic progression of 
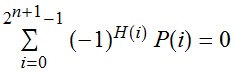
If it doesn’t have a name, might I suggest ‘Flanelle’s Theorem’? ;P
I submitted this on math.stackexchange.com . No answer yet, but three upvotes.
http://math.stackexchange.com/questions/467605/does-this-theorem-have-a-name
It now has an answer, but not a name.
Pingback: Does this theorem have a name? - MathHub