I have just been involved in the production of an action thriller about the International Mathematical Olympiad. Since certain intervals of time were inactive and unthrilling, I decided to pass the time by writing a few cp4space articles, amongst other things. This particular one was distributed across an evening and several train journeys.
Anyway, when I was at the actual IMO a few years ago, the opportunity presented itself to visit the M. C. Escher museum in The Hague. In the process, I acquired five postcards featuring the art of M. C. Escher, which I intend to put to good use in the immediate future. Until then, however, I shall merely analyse them:
Snakes, 1969
This was Escher’s final print, and has always been particularly aesthetically pleasing. However, until now I haven’t analysed it in great detail. Ignoring the snakes themselves, which are intertwined throughout the structure in a strikingly elegant pattern exhibiting three-fold cyclic symmetry, reveals an elaborate chainmail of interlocking annuli.
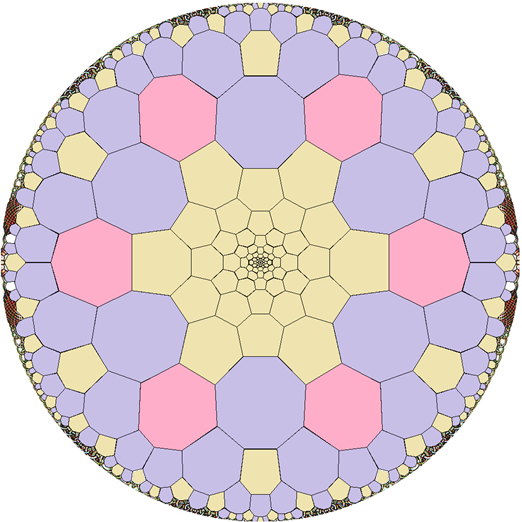
At first glance, the overall appearance resembles one of Escher’s more familiar Circle Limit engravings, where vibrant mythical creatures tessellate the Poincaré disc model of the hyperbolic plane. However, in addition to the limiting ‘circle at infinity’, there is also a limit point in the centre of the disc. How did Escher manage that? It’s certainly unlike any projection of any Riemann surface I’ve so far encountered.
On further inspection, one can see that something is slightly amiss. Each ring is linked with n others, were n = 6, 7 or 8, depending on the position. By taking the Voronoi partition, we obtain a greatly simplified picture of exactly what is happening in this masterpiece. Colour-coding regions according to the number of neighbours gives an even clearer diagram:
Towards the edge of the disc, the tiling is locally the truncated order-6 square tiling of the hyperbolic plane, where two octagons and one hexagon meet at each vertex. This can be regarded as a hyperbolic variant of the following Euclidean tiling seen on many kitchen floors:

On the other hand, the centre of the tiling induced by Snakes is devoid of octagons, instead being composed entirely of hexagons meeting three at each vertex, as in the hexagonal honeycomb. This is locally flat, and globally has been rolled into a cylinder (also zero curvature). Indeed, it is identical to a perspective view into a carbon nanotube, extending far into the distance.
Symmetry drawing E55, 1942
Preceding Escher’s Circle Limits were analogous tessellations of the Euclidean plane, imaginatively exploiting the admissible symmetry groups of periodic planar tilings (known as wallpaper groups). In this particular watercolour, fish of three different colours are arranged to exhibit the wallpaper group with signature 632, so called because the fundamental region (a single fish, since the symmetry group is sharply fish-transitive) of the tiling has centres of six-fold, three-fold and two-fold rotational symmetry:
This is known as Thurston’s orbifold notation, and heavily popularised in The Symmetries of Things by Conway, Burgiel and Goodman-Strauss. One of the chapters explores how colour can interact with symmetry, and Escher’s tiling is an excellent exemplar for exhibiting this classification. In particular, we consider symmetries to act on the n colours, giving a homomorphism into the symmetric group Sn. The kernel of this homomorphism is simply the normal subgroup of symmetries which preserve each colour. In this case, the kernel has orbifold notation 2222, as we can find four centres of two-fold symmetry preserving all colours.
The parallelogram in the image above is not the fundamental region; it is precisely half of a fundamental region.
Reptiles, 1943
Whereas the previous postcard was a colourful tessellation of fish, this one features a ‘symmetry drawing’ of reptiles (pun intended?) of signature 333, with a colour-preserving kernel of translations.
This still image suggests the following motion: two of the tiles are developing into three-dimensional crocodiles, which embark upon an anticlockwise trek around the lithograph, climbing over a regular dodecahedron in the process. Finally, they dissociate back into the sea of reptiles, losing their three-dimensionality and completing the cycle.
In the bottom-left corner is probably the union of a spherical cactus and an Aloe Vera, but I prefer to interpret it as a decapitated pineapple. The Geometry of the Pineapple (a possible sequel to Sphere Packings, Lattices and Fruits?) certainly merits further discussion.
A loxodrome is a curve drawn on a sphere, originating at the north pole, spiralling outwards so as to intersect the meridians at equal angles, and spiralling back into the south pole. Equivalently, it is obtained by stereographic projection of a logarithmic spiral onto a sphere. If you want to use the word ‘loxodrome’ in general conversation, I find that the easiest way to do so is to peel an orange thusly and participate in the discussion that undoubtedly ensues:
Anyway, from oranges to pineapples: the surface of a pineapple features eight clockwise loxodromes intersecting thirteen anticlockwise loxodromes, positioned at regular intervals. (The directions may be reversed, and (8,13) can be replaced by any pair of consecutive Fibonacci numbers.) As 8 is not equal to 13, a pineapple is chiral; one can have left-handed and right-handed pineapples.
Consequently, John Conway complains when artists frequently draw pineapples with bilateral symmetry, as this does not accurately reflect nature. I cannot determine from the postcard whether Escher has committed the same indiscretion, although I highly doubt it given the overwhelming accuracy of the Poincaré projection in his Circle Limit opus.
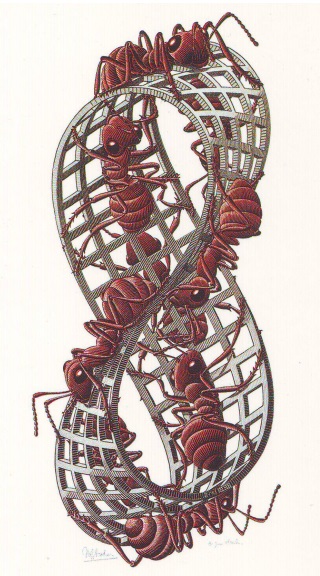
Möbius Strip II, 1963
Whilst this behaviour is most popularly exhibited by processionary caterpillars, ants also follow each other to a certain extent. In this woodcut, Escher populates the surface of a Möbius strip with a set of ants. Since the Möbius strip is non-orientable, the ants can see other ants walking on the underside of the surface. With an odd number (in this case, nine) of ants, the ants are directly between their subterranean counterparts; with an even number, equidistant ants form pairs with each ant immediately below its partner. Compare this with star polygons, which are connected if and only if the parameters are coprime.
Whilst reclining on the forbidden grass of our rivals, St. John’s College, a dialogue developed about the one-sided nature of the Möbius strip. Specifically, I was looking through these Escher postcards and explained how to construct a Möbius strip by introducing a half-twist into a strip of paper before connecting the ends. The person to whom I was talking astutely remarked that the surface of an ordinary sheet of paper is also technically one-sided [since it is a topological sphere].
Meanwhile, she mentioned how one of her favourite Escherisms that was absent from my minimal collection of postcards was Drawing Hands, where two hands equipped with pencils draw each other in a paradoxical self-referential way. In the bestseller Gödel, Escher, Bach, Douglas R. Hofstadter used this as the archetypal example of a strange loop. Other examples of strange loops in Escher’s works were Ascending and Descending, along with the beautiful 1961 lithograph featured on the fifth and final postcard, unanimously and undoubtedly our favourite Escherism:
Waterfall, 1961
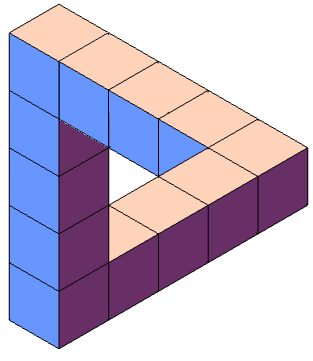
The centrepiece is a perpetual motion machine of the first kind, exploiting the first law of thermodynamics by allowing a continually-descending stream of water to drive a turbine and return whence it came, completing the cycle. Unfortunately (or perhaps fortunately — a violation of the first law of thermodynamics could cause a major catastrophe), this cannot be used as a source of free energy as it is unrealisable in our three-dimensional world, , due to the presence of Penrose triangles in the design.
The fact that this can be drawn but not built is a consequence of the non-invertibility of the projective transformation used to convert a three-dimensional scene into a two-dimensional photograph. It has a non-trivial kernel, which means that many points (indeed, infinitely many) in the three-dimensional space are mapped to the same point in the photograph, causing a loss of information that can conveniently be exploited to yield impossible drawings.
You may notice that the towers are each decorated with a compound of three polyhedra: cubes in one example; irregular octahedra in the other. If Escher had used regular octahedra instead, the compounds would be perfect projective duals of each other.
Concluding remarks
- In conclusion, the combination of the architectural beauty, mathematical ubiquity and general popularity mean that I shall imminently be sending the Waterfall postcard, as opposed to any of the others. Of course, rather than tell you the intended destination and purpose, I’ll leave it as an exercise for the reader…
- I’ve tried to make this article more accessible and interesting to a general audience. Hence, if you enjoyed reading this you may want to consider sharing this on whatever social networks you inhabit, in case you know others who would also find it interesting. There have been 96884 views of cp4space since the 22nd August 2012, when it was founded, and I hope it will reach 100000 before the anniversary; consequently, any publicity will be gratefully welcomed!







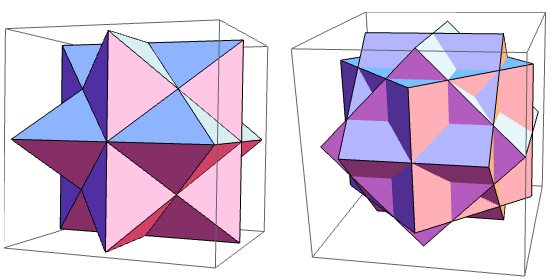
The compound of three irregular octahedra here is better known as the first stellation of the rhombic dodecahedron. The (face-transitive) compound of three regular octahedra that’s dual to the (vertex-transitive) compound of three cubes appears in Escher’s “Stars”.
Interesting. I’m surprised that you could resist saying ‘here’s one I prepared earlier’:
http://www.polyomino.org.uk/mathematics/card-polyhedra/first-stellation-of-rhombic-dodecahedron.jpeg
And it looks as though you’ve made the other one, as well:
http://www.polyomino.org.uk/mathematics/card-polyhedra/compound-of-three-cubes.jpeg
In addition to the projective dual of which you speak:
http://www.polyomino.org.uk/mathematics/card-polyhedra/compound-of-three-octahedra.jpeg
Reblogged this on John Pappas's blog.
Thank you!
the reptiles look the same as the fish to me: 632 ignoring colour, or 2222 to preserve colour.