In three dimensions, an aperiodic monotile is a solid capable of tiling space, but not in such a way that admits translational symmetry. The question of existence of aperiodic monotiles stems from a weaker question, which formed part of Hilbert’s eighteenth problem:
Does there exist a polyhedron capable of tiling space, but not tile-transitively?
The first example of an anisohedral tile was found in 1928 by Karl Reinhardt. An aperiodic monotile would obviously be anisohedral, although it surprisingly took 60 years before Schmitt found the first aperiodic example in 1988.
The purpose of this post is to present a new monotile I discovered a few days ago, and which seems like it could have been discovered much earlier than 1988. I also claim that its structure and proof of aperiodicity are simpler (i.e. easier to reconstruct) than any other aperiodic monotile.
Structure
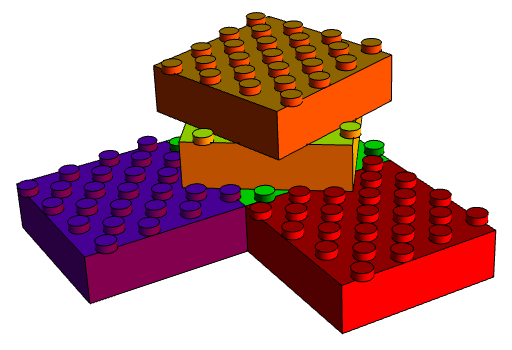
The aperiodic monotile is essentially a 5 × 5 Lego brick, where the grid of knobbles on the top (but not the complementary indentations on the bottom) have been rotated by the arctangent of ¾. Five such monotiles are shown in the diagram above. Four of the knobbles overhang, although reducing their diameter could overcome that. Similarly, if you prefer polyhedra to arbitrary solids, you can replace the cylindrical knobbles with square prisms.
Its existence stems from the Pythagorean identity 3² + 4² = 5², and this construction should generalise to any primitive Pythagorean triple. Of course, this is the simplest, and therefore the most preferable. Note that in this case, the knobbles on the top are in a centred square arrangement, rather than a square (and that relies on 3 and 4 being consecutive).
Proof
The only result that we’ll use is the fact that the Gaussian integers (complex numbers with integer real and imaginary parts) form a unique factorisation domain. This isn’t any more difficult to prove than the Fundamental Theorem of Arithmetic, which is the equivalent statement over the ordinary integers.
The first part of the proof is to show that the only tilings are the ‘obvious’ ones, where the monotiles form layers, each of which is a square lattice, and each layer is rotated by the arctangent of ¾ with respect to the layer below. Each tile forces tiles to exist above and below it, and rotated by this angle. This produces some overhang, which means that surrounding tiles are forced and (by induction) the entire tiling is arranged in layers.
The next part of the proof shows that no two layers have the same orientation. This is equivalent to showing that the complex number is not a root of unity. Suppose that it is a kth root of unity, in which case we obtain the identity
, which clearly violates unique factorisation. Hence, by a reductio ad absurdum argument, we win.
Consequently, if the tiling has any translational symmetry at all, it must be purely horizontal. We represent a translation by (x, y, 0) by the complex number z = x + i y. By considering the knobbles on one layer, we know that z must be a Gaussian integer (i.e. divisible by 1). By considering the knobbles on the layer above, z must also be divisible by . Considering all of these layers and using unique factorisation, we get that z is divisible by all integer powers of 2 + i, which is only the case for z = 0. So the tiling cannot have non-trivial translational symmetries, completing the proof of aperiodicity. Q. E. D.
Weakly versus strongly aperiodic
This monotile, together with Schmitt’s original monotile and the Schmitt-Conway-Danzer tile, can tile space screw-symmetrically. As such, it is described as weakly aperiodic. There are no known examples of strongly aperiodic monotiles (admitting no infinite cyclic groups of symmetries), but a step forward in this direction is the aperiodic monotile by Joan Taylor and Joshua Socolar.

If you were interested in using a crystal design for macroscopic self-replication purposes, one might want to build a cage of tiles surrounding a cavity, and then pour a liquid into the cavity – casting a new tile. If the tiles are somewhat compliant, you might be able to pour the liquid in via a narrow tube (a sprue?) running along a seam – but could the sprue perhaps be accomodated in the design of the tile?
I wouldn’t use aperiodic tiles for this purpose. Truncated octahedra form an elegant periodic tiling, and they don’t have structurally-dubious planar ‘cracks’ (c.f. http://projecteuler.net/problem=215 ) in the same way that the boring cubic honeycomb does. Another candidate is the rhombic dodecahedron.
As for your sprue problem, you could do it by having a semicircular valley on one face of the tile, and a complementary semicircular ridge on another face (for tiling and casting purposes). If you’re allowed to rearrange the tiles to remove the new tile from the cage, then this seems to be a valid solution. I’ll investigate this in greater detail shortly.
I was wondering how many faces would you need to make polyhedral aperiodic tile using this method, and I got an answer of 156, but two of sides would not be simply connected (would be “holey”). I started wondering if it is possible to modify your construction to get tiles without holey sides and with no two adjacent segments coplanar (e.g. two squares lying flat next to each other).
Your construction is impossible to translate to convex polyhedron, but is there any example of convex aperiodic tile? Or was it proven impossible? How about set of convex tiles?
The Schmitt-Conway-Danzer tile is convex and polyhedral, with eight faces:
http://demonstrations.wolfram.com/TilingSpaceWithASchmittConwayBiprism/
I don’t think there’s any significant difference between this tile and the others that admit screw-symmetric tilings. If anything, it just introduces extra complexity compared to constructions where an arbitrary irrational rotation angle can be used.
Warren Smith remarked that this has the property that the union of finitely many layers is periodic, whereas this is not the case for the Schmitt-Conway-Danzer tile.
Pingback: A more aperiodic monotile | Complex Projective 4-Space