Usually, it is very difficult to find a reasonably naturally-defined sequence which is not present on the Online Encyclopedia of Integer Sequences. The OEIS contains everything from the ubiquitous Bernoulli numbers and the fascinating Golomb self-referential sequence, to such utterly pointless trivialities as A171056 (the primes, but where every ‘7’ is replaced with a ‘9’ and vice-versa in the decimal expansions). More examples on the entire spectrum were competitively evaluated over at the Aperiodical.
Hence, I was rather surprised to see that the following sequence does not feature:
2, 6, 14, 22, 30, 34, 38, 42, 58, 66, 70, 78, 86, 94, ...
The motivation for this sequence was the observation that the numbers {2013, 2014, 2015} are each squarefree and have three prime factors. Ignoring the second condition, we can consider runs of consecutive squarefree numbers. Clearly, the longest such runs have length 3 (as in this example), since no multiple of 4 can possibly be squarefree.
- Definition: A positive integer N is described as comfortably squarefree if N − 1, N and N + 1 are all squarefree.
It is not difficult to obtain an infinite product expansion for the asymptotic density of comfortably squarefree numbers. An integer N is comfortably squarefree if and only if for every prime p, the residue of N modulo p² is not in the set {−1, 0, 1}. With a slight amount of work, this leads to the following asymptotic density:
If that 3 is replaced with a 1, it yields the density of squarefree integers, . Unfortunately, this does not appear to have a closed form. Numerically, I have evaluated δ ≈ 0.125486980906, where the final digit may be slightly off. Plugging this into Robert Munafo’s RIES doesn’t return anything, which is a shame as it is usually good at finding these sorts of things.
Even more bizarre is the fact that pairs of consecutive squarefree numbers have been investigated, mentioned at the end of the MathWorld article, and heavily featured on the OEIS. Hence, not believing that triples of consecutive squarefree numbers could possibly be a new concept, I searched this on Google (yes, this came after deriving the asymptotic density and numerically computing it!) and sure enough there was a MathOverflow question asking whether there are infinitely many examples.
Anyway, I’ll upload the sequence of comfortably squarefree numbers to the OEIS tomorrow, assuming no-one beats me to it.

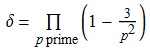
I noticed that mentioned density of squarefree numbers us exact same as density of relatively prime pairs. That suggested me that there might exist some natural bijection between these sets. Is that the case?
Sort of, yes. There’s a beautiful ring called the Profinite Completion of the Integers, which generalises the integers whilst preserving many number-theoretic properties:
http://groupprops.subwiki.org/wiki/Profinite_completion_of_the_integers
We can think of a number n in the Profinite Completion of the Integers as being the set of (n mod M) for every positive integer M, with the constraint that any finite subset of these residues must be consistent with each other. So you can’t have n being both (0 mod 3) and (1 mod 6), because they contradict each other.
But there’s nothing wrong with n being (0 mod 2), (1 mod 3), (1 mod 5), (1 mod 7), (1 mod 11), (1 mod 13), (1 mod 17), (1 mod 19) etc. Even though no integer satisfies all of these constraints simultaneously, any finite subset is consistent.
And in the Profinite Completion of the Integers, it’s easy to define a very natural bijection:
with the properties you describe. Specifically, by the Chinese Remainder Theorem we have that is just a direct product of non-interacting rings of p-adic integers (one for each prime p). In each of these rings, we define
is just a direct product of non-interacting rings of p-adic integers (one for each prime p). In each of these rings, we define  to be ‘interleave the digits of the p-adic expansions’. Then the full bijection f is obtained by doing all of these p-adic bijections ‘in parallel’.
to be ‘interleave the digits of the p-adic expansions’. Then the full bijection f is obtained by doing all of these p-adic bijections ‘in parallel’.
Now, we have the property that you wanted: pairs of relatively prime numbers are bijected with the squarefree numbers. But these numbers are elements of the Profinite Completion of the Integers, rather than the traditional integers.
Very interesting, I never knew this extension of integers exists. I hardly wrap my mind around p-adic integers, so maybe I’ll get into that topic some day else.
Also, I found sequence A007675 in OEIS, which are numbers exactly one less than comfortably squarefree integers.
Hmm, I was also informed of the existence of A007675 during the reviewing process for A228649:
https://oeis.org/draft/A228649