You have probably encountered the 15-puzzle, where all but one of the squares of a 4 × 4 grid are occupied by counters. The only acceptable moves are to move a counter into an adjacent unoccupied square.
Sam Loyd challenged people to swap a pair of adjacent counters. It is relatively easy to show that this is impossible, as changing the parity of the permutation of the sixteen objects (fifteen counters and one empty space) also changes the parity of the position of the empty space.
Unlike the Rubik’s cube, the set of positions in this puzzle do not form a group. Instead, they form a groupoid, since two operations can only be composed if the final position of the empty space in the first operation is equal to the initial position of the empty space in the second operation. Groupoids have the same axioms as groups, except for totality; it is not always possible to compose two arbitrary elements.
Conway, Elkies and Martin created a similar, albeit more interesting, puzzle. Place a counter on each of 12 of the 13 points of the projective plane of order 3. The plane has 13 lines of four points, and the following operation is allowed:
- Select a counter, move it into the empty space, and swap the two remaining counters on that line.
The groupoid generated is known as M13, since it has connections with the Mathieu groups. In particular, the subgroup of positions fixing the empty space is isomorphic to M12. M12 itself has been realised as the group of positions accessible with a mechanical puzzle. In fact, I know of at least three such descriptions, which are completely different:
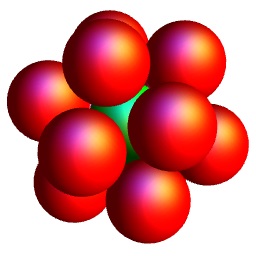
- Twelve ball-bearings touch a central sphere in an icosahedral arrangement. M12 is generated by pairs of clockwise and anticlockwise twists (where we choose an equator orthogonal to a diameter joining opposite spheres, and rotate one of the two hemispheres).
- The Number Planet mechanical puzzle by Oskar van Deventer and Jim Stasheff:

- The Topsy-Turvy puzzle, also by Oskar van Deventer:
[youtube=http://www.youtube.com/watch?v=H8ZcYvU0sLY]
There are electronic implementations of M12, M24 and Co0 as puzzles, designed by Igor Kriz whom you may recognise from his work in Euclidean Ramsey theory.


I understand “Representation Theory” to mean “Study of the representation of group operations by matrix multiplication”. In these puzzles, the (initially atomic) group operation is split into (admittedly, coupled) operations on local parts of the puzzle. Is there a connection to representation theory? Or is there a variant theory which one might call “representation by puzzles” or “representation by coupled automata” theory, which is simply difficult to google because of the dominance of the usual linear algebra sense of “representation”?
These are called `permutation representations’, which are special cases of linear matrix representations.
Pingback: Yf and only Yf? | Complex Projective 4-Space