As mentioned in a previous post, a pyritohedron is a (not necessarily regular) dodecahedron with pyritohedral symmetry. Up to scaling, any pyritohedron can be parametrised with the following coordinates:
- (±1, ±1, ±1);
- (±x, ±y, 0) and permutations thereof.
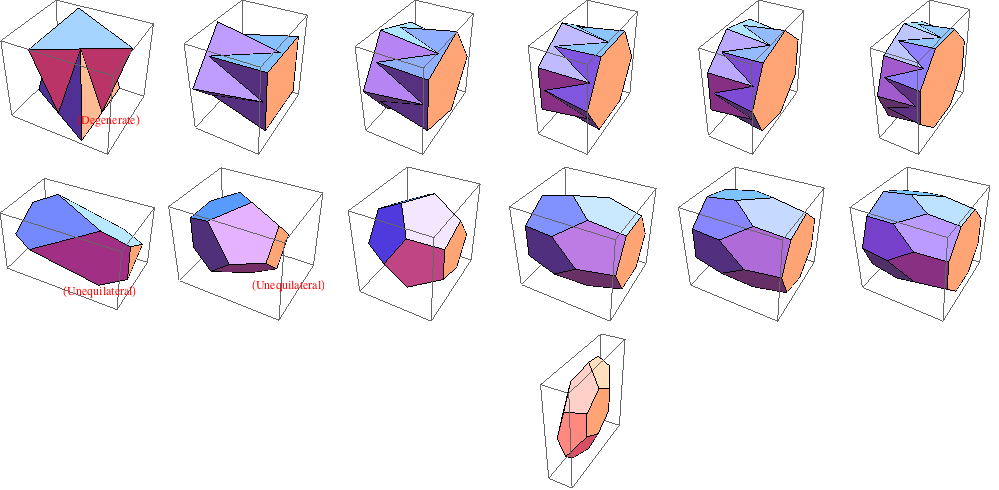
For the faces to be planar, we have a further constraint, Evaluating a basic 4-by-4 determinant gives the equation 2y = x + y², reducing the family of pyritohedra to have a single degree of freedom, h, where x = 1 − h² and y = 1 + h. Since there is only one degree of freedom, Bill Gosper realised that is particularly conducive to immortalising in a beautiful GIF animation, which he (for reasons unbeknown to me) entitled pyrominia.gif:
Let’s discuss each of these forms in further detail.
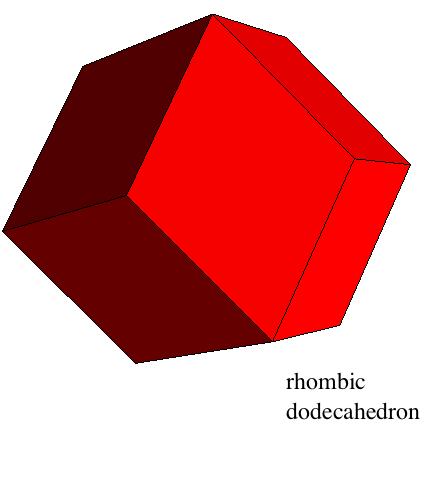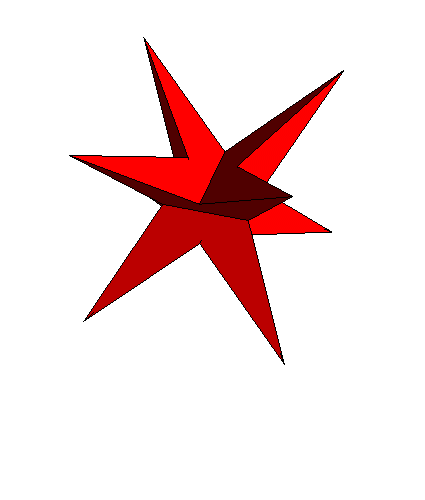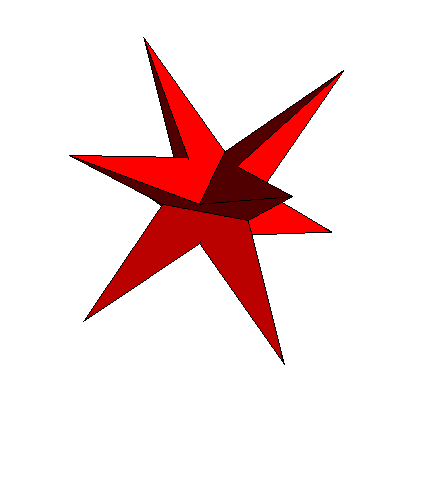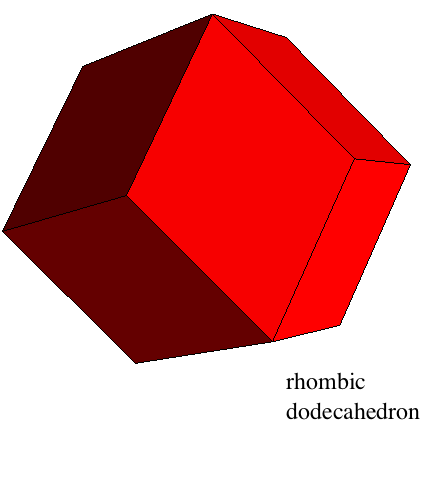
- We begin with the rhombic dodecahedron, a face- and edge-transitive polyhedron capable of tiling space in a face-centred cubic lattice arrangement. More precisely, it is the Voronoi cell of the lattice, that is to say the set of points closer to the origin than any other lattice point. Its projective dual is the cuboctahedron, one of the Archimedean solids.
- Next in the sequence is the well-known regular dodecahedron, one of the Platonic solids. Although the crystallographic restriction theorem precludes it from occurring in periodic crystals, there are pyritohedral approximations in iron pyrite (hence the name) and exact dodecahedral symmetry in certain quasicrystals.
- Not explicitly mentioned in pyrominia is one of the cells of the Weaire-Phelan structure. This is a more optimal soap bubble foam than the tessellation by truncated octahedra, the Voronoi cell of the body-centred cubic lattice (falsely conjectured by Lord Kelvin to be optimal).
- This is followed by the cubically degenerate pyritohedron, which marks the boundary between convex and concave pyritohedra.
- Next is the endo-dodecahedron. If you attempt to tessellate regular dodecahedra in the same arrangement in which one would usually tessellate rhombic dodecahedra, there is a small amount of empty space left over. The shapes of the holes are endo-dodecahedra, which are equilateral (all edges are of equal length).
- Eventually we reach the axes degenerate pyritohedron, beyond which the pyritohedra are self-intersecting.
- This is followed by another regular polyhedron, the great stellated dodecahedron. It is classified as a Kepler-Poinsot polyhedron rather than a Platonic solid, as it is self-intersecting and the Schläfli symbol (abbreviated form of a linear Coxeter-Dynkin diagram) has fractional values: {5/2, 3}.
Dihedral symmetry and pentiprisms
Julian Ziegler-Hunts discovered an irregular equilateral dodecahedron with dihedral symmetry, known as the pentagonal tympanohedron. It belongs to one of two infinite families of so-called pentiprisms (again a Gosperism), which resemble antiprisms but with pentagonal faces as opposed to triangles. The concave and convex families of pentiprisms are homeomorphic, as can be seen in this diagram (also by Gosper):
There is an exceptional hexagonal pentiprism, which is much flatter than the ordinary convex hexagonal pentiprism. Anyway, a few minutes ago Gosper created another animation, namely showing a deformation between a regular dodecahedron and the pentagonal tympanohedron:

Unfortunately, these dihedral forms are not as interesting as the pyritohedra. Nevertheless, half of the exceptional hexagonal pentiprism also occurs within the truncated triakis tetrahedron:
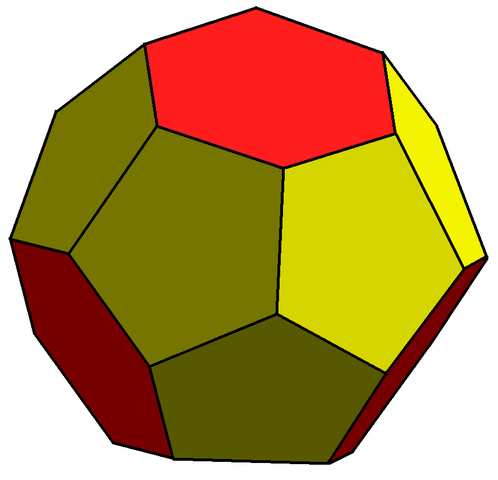
Do not be fooled into thinking that these faces are regular. If they were, we would have a Johnson solid. However, it is not possible to realise this in Euclidean space with regular faces, so it is known as a near-miss Johnson solid. Also be aware that the adjectives do not commute; a triakis truncated tetrahedron is a completely different solid (the Voronoi cell of the atomic structure of diamond), as mentioned in its Wikipedia article.
Incidentally, I seem to recall that I’m actually responsible for this confusion, as prior to a discussion between Tim Hutton and me, no-one had bothered to name this solid (despite it featuring in The Symmetries of Things). Following the standard nomenclature for systematically naming polyhedra, I entitled it the triakis truncated tetrahedron. Not long after, Tim Hutton created the Wikipedia article along with another for the corresponding tessellation.

This particular discussion spawned from Tim’s investigation of three-dimensional honeycombs on which to simulate reaction-diffusion systems and cellular automata. Tim was recently commissioned to use Ready to design a 40-foot bear sculpture with a reaction-diffusion texture!
Obviously, it inhabits a Baire space…


On the beginning, you wrote “single degree of freedom, h, where x = 1 − h² and x = 1 + h.”. I believe latter one should be y = 1 + h.
Excellent point.
It is also possible to continue past the rhombic dodecahedron to obtain a self-intersecting equilateral dodecahedron that looks like a (convex) regular dodecahedron with six digonal disphenoids attached to it.