Yf and only Yf?

There are plenty of triangle centres. One of the lesser-known triangle centres is Kimberling’s X(174), the Yff centre of congruence. It can be defined by considering lines known as isoscelisers, which are lines perpendicular to the angular bisectors of the triangle. If we’re careful, then they can intersect in such a way that three of the triangles formed (by an edge of the triangle and the isoscelisers of the two adjacent vertices) are congruent. This gives a degree of freedom:

The Yff central triangle is the case where the triangle formed by the three isoscelisers (red) is also congruent to the other three. When this triangle vanishes, we obtain the Yff centre of congruence. Apparently they’re named after their discoverer, Peter Yff, who was responsible for discovering several other triangle centres.

In particular, he rediscovered the second Morley centre. Morley’s theorem is quite a subtle result in Euclidean geometry, not least because the points concerned cannot be constructed by Euclidean methods. More precisely, they lie outside the field containing the vertices of the triangle and closed under the operation of taking geometric means. Anyway, the statement of the theorem is as follows:

Consider a triangle ABC. We form the point A’ by letting the angle trisector of ABC (closest to BC) meet the angle trisector of BCA (closest to BC). We similarly define B’ and C’. Then A’B’C’ is an equilateral triangle.

This is called the first Morley triangle. I seem to recall that if you take a cardioid inscribed within ABC, then its centre will lie on the perimeter of A’B’C’, and indeed the perimeter of A’B’C’ is the locus of possible centres. There’s a paper exploring this property and its relation to certain interesting cubics* in the plane of the triangle.

* You’re probably familiar with ‘interesting points’ (namely triangle centres), ‘interesting lines’ (such as the Euler line) and ‘interesting circles’ (the incircle, circumcircle, Euler-Apollonius lollipop etc.). In the same fashion, there are conics, cubics and higher-order algebraic curves passing through plenty of triangle centres.

Anyway, if we chose the other two angle bisectors and joined them, we would get a point A” opposite A’. Then, the triangle A”B”C” is also equilateral (it follows from the fact that, algebraically, it is defined in precisely the same way as the first Morley triangle), and called the second Morley triangle.

It can be shown that ABC, A’B’C’ and A”B”C” are in pairwise perspective (Desargues-style!), so we obtain three more points, P, Q and R, as perspectors. Taking these twelve points together with the nine lines of perspective and three of the original angle trisectors gives a self-dual projective configuration of 12 points and 12 lines discovered by Zacharias.

But then we can form its incidence graph! This is a bipartite symmetric cubic (3-regular) graph known as the Nauru graph. The etymology of this graph is derived from its drawing as a generalised Petersen graph, whose interior star polygon resembles the 12-pointed star on the flag of Nauru:

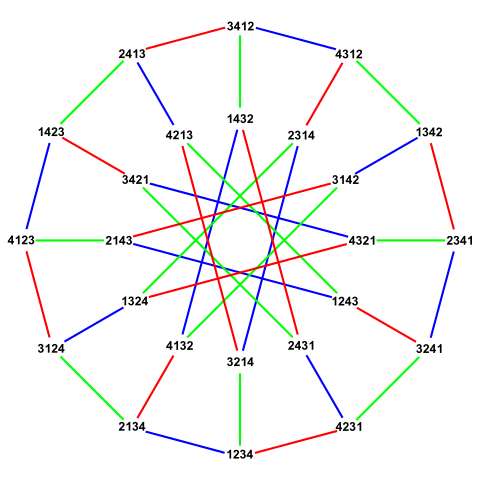
So, I guess it’s appropriate to explain the labels and coloured edges. We can think of this as the Cayley graph of the group S4 (with generators corresponding to transpositions (1 2), (1 3) and (1 4)), or as the map of admissible moves in a corresponding groupoid puzzle. I’ll describe the latter. We have four pedestals, each capable of accommodating precisely one Ferrero Rocher, of which we have one of each of three varieties. Then, on each move we can select a Ferrero Rocher and move it to the unoccupied pedestal. The graph of positions where edges correspond to legal moves is then the Nauru graph.

The Nauru graph has many other interesting properties such as symmetrical embeddings on a torus. David Eppstein investigated how these aspects are connected, and developed a theory of xyz graphs (basically cubic graphs that can be embedded as (possibly self-intersecting) orthogonal polyhedra). He has a series of articles on this topic, which, despite being on the same website, do not appear to share an index page. Hence, I’ll link to them here in chronological order:

1. Inverted permutohedron, exhibiting the first example of a xyz graph.
2. A projective plane in a 3d grid, which defines the concept of an xyz graph and explores a particular example, which is shown (by the easy classification of surfaces according to orientability and Euler characteristic) to be homeomorphic to the real projective plane.
3. Topology of xyz graphs, which expands on the previous ideas and realises all such compact surfaces (which can be formed by gluing finitely many handles and crosscaps to a sphere, as shown in The Symmetries of Things) as surfaces of immersions of xyz graphs.
4. 3-colouring and xyz graphs, which gives (rather beautiful) necessary and sufficient conditions for one to be able to convert a graph drawn on an abstract topological surface back into an immersion of an xyz graph, rather than the usual reverse process.
5. st-orientation and xyz graph recognition, which mentions the theory behind an exponential-time algorithm for recognising xyz graphs.
6. Ambiguously xyz, which exhibits an xyz graph that can be immersed in two distinct ways. It is proposed that this could be used as a method for reducing NP problems into the problem of determining whether a graph is an xyz graph, thereby strongly suggesting that there are no polynomial-time to perform xyz graph recognition.

Roughly at this point, he published the material in the form of a paper. However, later posts appeared, particularly involved with cubic symmetric xyz graphs (such as the Nauru graph itself). Indeed, we have:

7. Cubic symmetric xyz graphs, which is fairly self-explanatory.
8. More on cubic symmetric graphs.
9. The many faces of the Nauru graph, investigating embeddings on hyperbolic surfaces.
10. Not the Nauru graph.