Many theorems in analysis have combinatorial analogues, which turn out to be equivalent (in the sense that one can be derived from the other, and vice-versa, using significantly less maths than is necessary to prove either from first principles). A particularly useful theorem is Brouwer’s fixed-point theorem, which can be proved from its combinatorial discretisation, Sperner’s lemma.
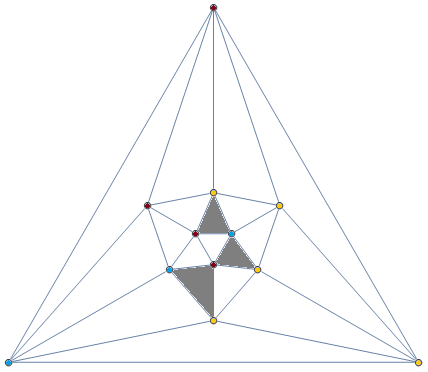
Sperner’s lemma, not to be confused with the similarly-named theorem generalised by Hunter as mentioned in my earlier article about punting in clearings of arbitrarily small Lebesgue measure, is concerned with colouring vertices in a simplicial subdivision of a simplex. In two dimensions, we take an equilateral triangle and cut it into smaller triangles, like so:
We colour each of the vertices with one of three colours (or n + 1 for the n-dimensional version), such that all of the vertices of the original triangle (or simplex) are different colours. Also, if a vertex occurs on the boundary of the simplex, then it must be coloured with the same colour as one of the vertices of the facet in which it resides. (So, for example, any vertices on the bottom edge of the triangle above must be either blue or yellow.)
Then, Sperner’s lemma states that the number of triangles (or simplices) in the subdivision whose vertices are distinct colours (highlighted in grey in the diagram above) is odd. Crucially, that means that there must be at least one such simplex.
In one dimension, the lemma is completely trivial to prove. It states that if we have a finite sequence of vertices coloured red or blue, such that the leftmost vertex is red and the rightmost vertex is blue, then there are an odd number of pairs of adjacent differently-coloured vertices. For instance, the following diagram has five such edges, highlighted in yellow:
Proving Sperner’s lemma involves inducting on the number of dimensions. For instance, the two-dimensional statement can be deduced from the (trivial) one-dimensional statement. We consider the triangulation to be drawn on the surface of a sphere (so the large triangle also constitutes a triangle), and form a subgraph of the dual polyhedron by replacing each triangle with a vertex and connect vertices corresponding to triangles sharing an edge whose endpoints are (red, blue). Now, by Sperner’s lemma in one dimension, the big triangle has odd degree. Hence, by the handshaking lemma, we can find another triangle with odd degree, which must correspond to a triangle where all vertices are differently coloured.
As well as its use in proving Brouwer’s fixed point theorem (mentioned below), Sperner’s lemma is involved in the proof of Monsky’s theorem, that we cannot dissect the unit square into an odd number of triangles of equal area. The proof is reasonably short, but amazingly ingenious. I very much recommend reading it.
Analytical analogue
We aim to prove Brouwer’s fixed point theorem, which states that any continuous function from the closed n-ball to itself must necessarily have a fixed point. An equivalent problem is to show that there is no continuous function f from the closed n-ball to its boundary S such that f restricted to S is the identity function (such an f is called a continuous retraction).
We shall demonstrate this for simplicial subdivisions of regular simplices, which are homeomorphic to balls, and intend to show that any continuous function f sending vertices to vertices (a simplicial map) that is the identity when restricted to the boundary must send one of the simplices in the subdivision to the big simplex.
In particular, let the vertices of the big simplex be {v_0, v_1, v_2, …, v_n}. Then we give a generic vertex w the colour i if f(w) is closer to v_i than any other v_j. After taking a deep breath, we realise that any continuous retraction must violate Sperner’s lemma, thus establishing that continuous retractions do not exist for simplicial subdivisions of regular simplices. And since any continuous function can be approximated by considering its effect on a sequence of progressively more refined simplicial complexes, we are done.
The special case of Brouwer’s fixed point theorem applied to homeomorphisms in three dimensions has a nice physical interpretation. Suppose we have a volume of pumpkin velouté in a glass vase, and stir it crazily in a continuous way. Then the fixed point theorem states that somewhere, a molecule of the velouté is in the same place whence it began.
Midsummer House
Speaking of pumpkin velouté, that was, when punctuated with a la grecque mushrooms and Parmesan gnocchi, the first of eleven courses in a most delightful meal I enjoyed at Midsummer House on Thursday evening. Ordinarily, cp4space does not usually give reviews of double-Michelin-starred restaurants in articles about combinatorial proofs of analytical theorems, but this time I shall make an exception.
Not only was the food incomparably excellent, but also the atmosphere was absolutely perfect. We were seated on two extraordinarily comfortable chairs in the spacious solarium of a quaint Victorian villa overlooking the Cam. The ambient illumination was provided by contemporary candelabra situated around the boundary of the room, providing a warming glow on this late November evening.
Before the amazing dinner began, we were given champagne, canapés* and condiments, the latter of which had, in the case of the other person with whom I was dining, an unusually overwhelming affinity for the table cloth. Fortunately, its act of rebellion was expertly rectified by the means of a supplementary table cloth provided after the course of pumpkin velouté, when its disobedience became known to the brilliantly professional staff.
* Miniature cheese scones and suchlike. I would have added this in parentheses, but decided that a footnote allowed me to do so without interrupting the alliteration.
The second course encompassed mackerel tartare, chervil, fennel and passion fruit, arranged in an aesthetically pleasing symmetrical configuration. This was accompanied by the first of a flight of wines designed to perfectly complement the exquisite dishes.
This was followed by great confusion when a large metal trolley arrived; we were assured that the explanation as to its imposing presence would become apparent in the immediate future. Due to unbridled inquisitiveness, I was compelled to consult the menu to deduce its purpose in life, correctly inferring that it harboured the ‘open coals’ on which the beetroot was to be cooked.
Unsurprisingly, the beetroot was extremely flavoursome, and by far the best beetroot I had ever had the fortune to sample. Indeed, this statement would remain true if ‘beetroot’ were to be replaced by many of the other culinary delights on the menu. Including the course of sautéed scallop, celeriac and truffle. The celeriac was arranged in alternating layers of parallel lines, forming a precise Cartesian grid when viewed from above.
According to the menu, the next course comprised roast quail, shallot purée, grapes, celery and sour dough, positioned on various strata of an interesting bowl, the structure of which was analogous to the discrete energy levels occupied by an electron in a hydrogen atom. This was accompanied by a pleasant surprise, namely the delicacy of quail’s eggs. Unlike most eggs, which are conventionally and eponymously ovoid*, these were spherical. The interior was a luscious yolk.
* The most common explanation for the deviation from a sphere or prolate spheroid is so that, when rolled, the egg travels in a closed path rather than escaping arbitrarily far from the origin and falling from the bird’s nest; this presents an evolutionary advantage.
For the following course, we had a choice between bass and monkfish, and decided upon the latter on the basis that I was already accustomed to the taste of bass. When asked what monkfish was, and due to the temporary cognitive modification that results from having consumed considerably more wine than my opponent, I bluffed with total conviction that they are marine animals, which live totally detached lives in monasteries (and in the immortal words of Meat Loaf, two out of three ain’t bad). She was not fooled by this ruse.
I distinctly remember quince appearing on the menu, as I was asked to describe it and quite satisfyingly was able to respond with ‘a fruit with botanical name Cydonia oblonga‘. (The reason for knowing the Linnaean name of a quince is another story, involving a friend of mine called Quincy, and is far too tangential to describe here.)
The next course was a pousse café, a delicious combination of several liquids of distinct densities, which formed strata in a hemispherical receptacle atop a glass vessel. The uppermost layer, which was delightfully creamy, was peppered with fragmented mint leaves. This was followed by a range of artisanal cheeses.
The penultimate course was an indescribably delectable dessert of lemon posset, lemon espuma and blueberries. In fact, it was so amazingly orgasmically excellent that it would be assigned some non-recursive transfinite ordinal on Vishal Patil’s famous dessert quality scale, which hitherto only ranged from 0 to 10.
The eleventh and final course included caramel, chocolate and chestnuts (ooh, another triple alliteration!), providing an ideal culmination for this fabulous gastronomic experience. It was accompanied by a sweet dessert wine, the seventh of the glasses in the flight of wines, which complemented the course perfectly.
At the end of the meal, which was over three hours of absolute Elysium, we spent a rather long time exploring the balcony, overlooking the river (which would have been moonlit had I had the foresight to ensure that the evening coincided with the correct lunar phase), and enjoying the satisfyingly secluded gardens of this Victorian villa, until ultimately retreating into the Fellows’ Garden of Trinity College…
So, yes, I thoroughly recommend this splendid restaurant. The Empress of TMAS described it as:
‘The nicest forfeit I’ve ever been on’
(Specifically, she agreed to do absolutely anything in return for being removed from the freshers’ team for the Trinity Mathematical Society Call My Bluff — which you should definitely attend on Monday 2nd December — and I decided that this would be appropriately awesome.)
Borsuk-Ulam and Tucker’s lemma
Returning from that rather brief aside, there are other examples of theorems in analysis with combinatorial counterparts. In particular, the Borsuk-Ulam theorem (mentioned in Desert Island Theorems) has Tucker’s lemma as its discrete version.

That could be easily consumed just by downloading a few podcasts. To everyone else I would suggest they go with what they know, and stick with the i – Pad.
SPAM SPAM SPAM SPAM