(This article is about the axioms concerned with the existence of enormous sets. If you were instead looking for corpulent subordinates of the Pope, then I suggest watching this Monty Python sketch.)
How big is the universe? Ultrafinitists such as Doron Zeilberger reject the Axiom of Infinity, and only allow finite sets. The universe of all finite sets, Vω, is a perfectly consistent set theory, which obeys all of the other axioms of ZFC. It’s not a particularly powerful set theory, though, as we can’t encapsulate the notion of the set of natural numbers.
So, Vω is too small to be consistent with ZFC. It turns out that the smallest universe consistent with ZFC is L, Gödel’s constructible universe, where at each successor stage we take only the sets expressible by first-order formulae ranging over sets in the previous stage. In L, the generalised continuum hypothesis is true, so every cardinality can be obtained by taking unions and powersets. There are other nice corollaries of V = L (the axiom that the entire von Neumann universe is the same as Gödel’s constructible universe) such as the existence of a Suslin tree.
Large cardinals are those with special properties, typically whose existence is not implied by ZFC. Many of these have very complicated set-theoretic definitions, but there are some easier notions related to Ramsey theory. For example, for your favourite ordinal α, the Erdős cardinal κ(α) is the smallest cardinal such that for all n, every 2-colouring of the n-subsets of κ(α) contains a monochromatic set of order type α. If α = ω, for example, then the infinite Ramsey theorem asserts that κ(ω) = ![]() .
.
0# and beyond
Note that if β < α, then the existence of κ(α) implies the existence of κ(β). There’s a property of intermediate strength between the existence of κ(ω1) and the existence of κ(β) for all countable β, namely the rather interesting axiom 0#. 0# is defined as a set of true statements (in L augmented with the symbols {![]() ,
, ![]() , …} (one for each natural number) interpreted as cardinalities in V), but it can also be encoded as a set of naturals (by Gödel numbering) or indeed as a real number.
, …} (one for each natural number) interpreted as cardinalities in V), but it can also be encoded as a set of naturals (by Gödel numbering) or indeed as a real number.
The only problem is that sometimes statements do not necessarily have a prescribed truth value, so 0# is not necessarily well-defined. If 0# exists, then V is much larger than L; otherwise, V can only be very slightly larger than L. So, 0# is really the first large cardinal property that goes beyond V = L.
Beyond 0#, there is a hierarchy of increasingly strong large cardinal properties. At the end of this list are Reinhardt cardinals and strong partition cardinals, which are so strong that they break ZFC (although strong partition cardinals, at least, are consistent with ZF). The strongest large cardinal that is not known to be inconsistent with ZFC is a rank-into-rank cardinal, which is marginally weaker than a Reinhardt cardinal.
Specifically, it asserts the existence of an ordinal γ such that the γth iteration of the von Neumann universe, Vγ, can be non-trivially mapped into itself such that the truth of all first-order statements are preserved. (Such a map must obviously be an injection, as the statement ‘a is not equal to b’ must be preserved for all distinct elements a and b.)
Laver tables
The existence of a rank-into-rank was used by Richard Laver to prove a certain very combinatorial statement. A Laver table of order n is the table of a binary operation satisfying the properties
and
.
The periodicity of the first row of the Laver table, i.e. the period of as a function of i, must necessarily be a power of 2. In the example above (n = 2), the first row is (2, 4, 2, 4), which has a period of 2. The period is also an increasing function of n, but it increases extremely slowly. It (sequence A098820) begins as follows:
1, 1, 2, 4, 4, 8, 8, 8, 8, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, ...
where the number of sixteens is more than A(9), where A(n) is the fast-growing Ackermann function. In general, the point at which the sequence first exceeds 2^m, if it exists, is not a primitive-recursive function of m (eventually dominating the Ackermann function).
The proof that the sequence increases without bound actually relies on the existence of a rank-into-rank cardinal. So, if these things don’t actually exist (which is entirely plausible), then it may be that the sequence is eventually constant. It seems extremely unusual (impossible, surely?) that such a basic combinatorial statement would be independent of ZFC, so it is generally believed that A098820 does indeed grow without bound. But then again, it has not been proved that the existence of a rank-into-rank is consistent with ZFC, and people initially believed otherwise — that the inconsistency proof of Rienhardt cardinals could be adapted to disprove the existence of a rank-into-rank — but all attempts failed miserably so the general concensus is that they are consistent with ZFC.

If you Godel-encode a set theory with large cardinals, don’t you get something that ultrafinitists would be comfortable working with?
Unless I am mistaken, the question of whether large cardinals “exist” depends on what you mean by “exist”. The ultrafinitists would prefer to say that a mathematician manipulating large cardinals is manipulating symbols (which exist and are finite), and the set-theory realist would prefer to say that the ultrafinitist who claims to be manipulating symbols is actually manipulating some (perhaps inaccessible, situated on some dualistic plane of platonic forms) mathematical objects, and the symbols the ultrafinitist uses refer to those objects.
Is this merely an argument about terms?
Suppose you Gödel-encode a set theory such as ZFC, and the positive integers correspond to statements. Some of these will be provably true, others will be provably false, and there are lots of statements which can neither be proved nor disproved. It is meaningless to attribute a value of `true’ or `false’ to those integers.
Whereas in actual set theory before you subjected it to the mincer of Gödel-encoding, it feels as though a statement such as the continuum hypothesis should be either true or false, even though we can’t prove or disprove it with the ZFC axioms.
So, that’s where the philosophies of `mathematics is a formal game’ and `mathematics actually exists in some reality’ differ: whether they believe that unprovable statements should have assigned truth values.
Is there a name for binary operations * satisfying a * (b * c) = (a * b) * (a * c)?
A cool name for it would be “self-distributive” binary operation. But I think proper name would be “distributive over itself”
Well, self-left-distributive (or would that be right distributive). Also, what is known about such binary operations?
One of the formulas does not parse for me. I also think next one should say p*1=p+1 mod 2^n.
The formula that doesn’t parse (basically, WordPress is shockingly terrible at compiling LaTeX code) gives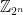 as the domain and codomain, so the `mod 2^n’ is implicit.
as the domain and codomain, so the `mod 2^n’ is implicit.
Ikea used to sell Laver Tables. They stopped selling them after people realized that to seat 32 people at one, you had to buy at least A(9,A(8,A(8,255))) chairs.
http://img.docstoccdn.com/thumb/orig/151075420.png
Haha, yes, Ikea have made it very difficult to search for Laver tables on Google images…
Let q(n) be minimal so that p(q(n)) = 2^n. I conjecture that q(6) is far larger than BH(3), SCG(13), or TREE(3).
We know that the function (if it even is a function — I’m not convinced that ZFC + rank-into-rank is arithmetically sound, or even consistent) outgrows the Ackermann function, but there’s no reasonable upper bound.
I don’t have any reason to see why it should outgrow BH, SSCG or TREE. It’s certainly a computable function (systematically test each Laver table and check for periodicity), so it’s definitely dominated by the Busy Beaver function.
The big question is: which ordinal corresponds to this function in the Grzegorzyck hierarchy? We have omega as a lower bound, and the Church-Kleene ordinal as an upper bound. If q(n) outgrows BH, then it would establish a huge recursive ordinal (the Buchholz ordinal) as a lower bound.
I’m mostly relying on intuition with fast-growing functions here. The Goodstein function can’t be proven total in PA (but it can in stronger systems), and its growth rate is measured by the proof-theoretic ordinal of that system, or epsilon_0. The BH function can’t be proven total in Pi11-CA0+BI (but it can in stronger systems), and its growth rate is also the proof-theoretic ordinal of that system, or psi(epsilon_(Omega_omega + 1)). q(n) can’t be proven total in ZFC + rank-into-rank (assuming that that actually works), and even if its growth rate doesn’t match up with the proof-theoretic ordinal of that system, I hope there’s some way we can extract a seriously powerful function out of this.
q(n) can be proved total in ZFC + rank-into-rank (and it has). I agree that if it can’t be proved total in ZFC, then it’s most probably much faster-growing than BH et cetera, but there isn’t any evidence that this is the case (I don’t even think that it has been proved independent of PA).
Of course, ZFC is much stronger than Pi11-CA0+BI, so a ZFC-independent combinatorial theorem would lead to an extremely fast-growing function.
Right, right. Thanks for clearing that up.
If you are interested in functions so extreme ZFC can’t prove them total, I recommend you this paper by Harvey Friedman: http://arxiv.org/abs/math/9811187 (I haven’t read it yet, but friend of mine has recommended it). In fact, propositions appearent in that paper are not only unprovable in ZFC, but, quoting the paper, they “imply the
consistency of ZFC+{there exists a k-subtle cardinal}_k”.
Pingback: Comprehending ultrafilters | Complex Projective 4-Space