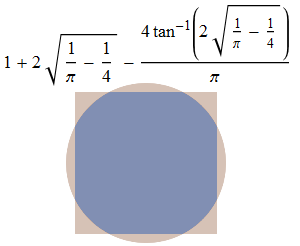Is it possible to dissect a square into finitely many pieces, which can then be rearranged to form a disc of equal area?
Note that, unlike in three dimensions where the Banach-Tarski paradox exists, dissections must respect the two-dimensional Banach measure and therefore preserve areas. Hence, it is impossible to rearrange the pieces to form a disc of larger or smaller area than the original square.
Obviously, if the pieces are sufficiently well-behaved (e.g. have simple piecewise-smooth boundaries), then there is no solution; the proof is extremely elementary. In 1989, Laczkovich found an axiom-of-choice-based dissection into approximately 10^50 pieces, answering Tarski’s question in the affirmative.
Anyway, my friend and colleague Tim Hutton, inspired by discussion with his 6-year-old daughter, decided to ask how close you can manage with n non-pathological pieces, for varying values of n. More precisely, he asked the following question:
What is the supremum area a(n) of n interiors of topological discs with piecewise smooth boundary, such that they can be packed in both a circle of unit area and a square of unit area?
It is trivial to observe that as n tends to infinity, a(n) monotonically approaches 1. Also trivial is establishing the value of a(1):
He’s also launched a collaborative project to find dissections giving lower bounds for a(n). For instance, with six pieces it is possible to achieve 0.9860:
Undoubtedly, more can be found on Tim Hutton’s Google+ page.