My favourite author, after whom I was named, is undoubtedly Douglas Adams. I particularly enjoyed Dirk Gently’s Holistic Detective Agency (sadly, not quite as famous as his bestseller, The Hitchhiker’s Guide To The Galaxy), featuring a rather disorganised and slightly unscrupulous Cantabrigian detective whose methods rely on the ‘fundamental interconnectedness of all things’.
It has been observed that I share several characteristics with Dirk, including an ability to predict exam questions (co-discovering the result of FST2 2012 Q2 several months before the paper whilst experimenting with determinants, thus trivialising the question for anyone with whom I had discussed the result), although fortunately (unlike in Dirk’s case) it did not result in expulsion from Cambridge. Also, we both famously share a penchant for fine wine and dining.
One of the themes in Dirk Gently’s Holistic Detective Agency involves a sofa* wedged in an awkward position in a tortuous staircase, from which it cannot be moved (and, since rigid motions have inverses, it was noted that it could never have even reached that position ab initio!). Dirk Gently’s assistant**, Richard MacDuff, was experimenting with a computer simulation capable of rotating the sofa in three-dimensional space to liberate it, eventually concluding its impossibility.
* Also known as a settee, couch, or Chesterfield. An example of the aforementioned ‘fundamental interconnectedness of all things’ is that I was born in Chesterfield, a town in Derbyshire whose most distinctive feature is a church afflicted by erectile dysfunction. Additionally, a Chesterfield sofa featured in one of Adams’ other novels, the identity of which I shall leave as an exercise for the reader.
** This position involves performing various tasks that Dirk is unwilling or prohibitively lazy to execute himself, and suffering frequent minor misfortune as a result of Dirk’s blithering ineptitude. I imagine that Maria Holdcroft can empathise with him, being attacked by a particularly temperamental pen that exploded as she was writing a cp4space advertisement, its volatility originating from when I accidentally left it in my trousers whilst they were subjected to the aquatic violence of a washing machine. Similarly, she had to drive 100 miles with a post-crapulent friend of hers after a rather convoluted and initially promising plan of mine failed spectacularly.
According to Wikipedia, the origin of the immovable sofa problem was an event that occurred whilst Douglas Adams was at St. John’s College, Cambridge (our rivals***). Specifically, when a particular staircase was renovated, furniture was temporarily placed in the upstairs rooms to allow the redecoration to take place. The renovation, however, made it impossible to remove the sofas from the rooms, so they remained there for decades!
*** As a result of this, the bridge over the stream between Trinity and St. John’s is permanently locked. This caused me to miss lunch on one occasion, but that’s another story…
Intriguingly, this physical problem was independent of Leo Moser’s moving sofa problem, which is a two-dimensional unsolved mathematical problem. It is of a similar vein to the problem that inspired my article about punting in clearings of arbitrarily small Lebesgue measure, but involves maximising the object rather than minimising the space. Specifically, Leo asks:
What is the maximum area of a sofa (connected subset of the plane) that can be manoeuvred around a 90° corner in a corridor of unit width?
Claudio Rocchini produced a beautiful animation of a lower bound established by John Hammersley (an Emmanuel College alumnus best known for developing the theory of Monte Carlo methods) in a paper entitled ‘On the enfeeblement of mathematical skills by ‘Modern Mathematics’ and by similar soft intellectual trash in schools and universities’:
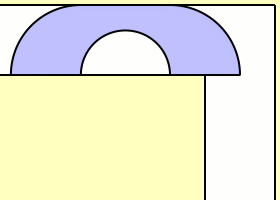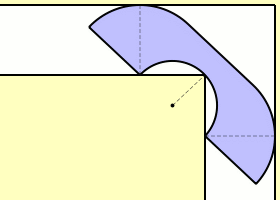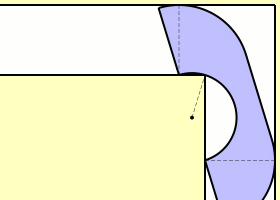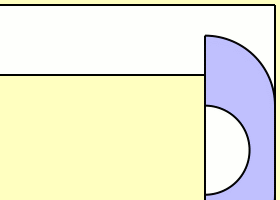
Amazingly, that is actually a reasonable shape for a sofa! The Hammersley sofa has an area of , which he conjectured to be optimal. According to private communication between John Conway and the about-to-be-mentioned Joseph Gerver, this was very slightly optimised to give a sofa with a larger area (the Shephard piano), which was in turn optimised by Richard Guy et al to achieve an area of 2.2156. Gerver then exhibited a sofa of area 2.2195 with piecewise-smooth boundary, which he conjectured to be [very close to] optimal.
Gerver, however, demonstrated something of far greater importance than a slightly improved lower bound, namely the existence of an optimal sofa (the alternative would be an unattainable supremum on the possible area). Specifically, he considered the topological space X of all possible sofas, and proved that there exists a compact subset J of X containing sofas arbitrarily close to the supremum. Then, by compactness, the image of J under the function mapping a sofa to its area must also be compact and therefore attain its upper bound.
This technique can be applied to many other optimisation problems in geometry to give optimal solutions. For example, given a polygon P in the plane, there is a largest circle that can be inscribed in P. (Proof: the subset of giving admissible locations and radii of circles is bounded by finitely many weak algebraic inequalities, so is compact. Proceed as in the previous argument.)
Anyway, the moving sofa problem is merely a special case of the piano mover problem.

In Germany, this book is known as “Der elektrische Mönch” (“The Electric Monk”). At first I was confused, remembering the sofa story from a completely different book by Douglas Adams, but then I noticed that it is the very same book (Dirk Gently’s Holistic Detective Agency).
I can highly recommend this book, especially for people who don’t have a lot of time. That book is very small compared to the Hitchhiker’s Guide, but no less amusing.
Yes, I remember that the Electric Monk featured quite prominently in the plot! Also, I agree entirely and second your recommendation.
I can tell a very interesting example of fundamental interconnectedness of all things. Namely, yesterday, it happened so one of our teachers tried to push a table through a door. When jokes about how he could’ve broken a wall for it to go easier, I mentioned to one of my friends there actually exists a mathematical problem connected to pushing things through corridors, and explained moving sofa problem.
The next day, on my favorite mathematical blog, an article about moving sofa problem appeared.
Coincidence?
Definitely another instance of the Fundamental Interconnectedness of All Things! 😀
I was actually looking for Gerver’s paper about existense of maximal sofa. Only one of his works which I found was concerning moving sofa problem: https://www.math.ucdavis.edu/~suh/gerver-moving_sofa.pdf
However, in this publication, Gerver wrote: “Later, Conway and M. Guy proved that a sofa of maximum area (not necessarily unique) exists”,. What Gerver proved in this paper is stronger result that there exists maximal sofa approximable by balanced polygons.
Pingback: A History of the Moving Sofa Problem – STEMantics