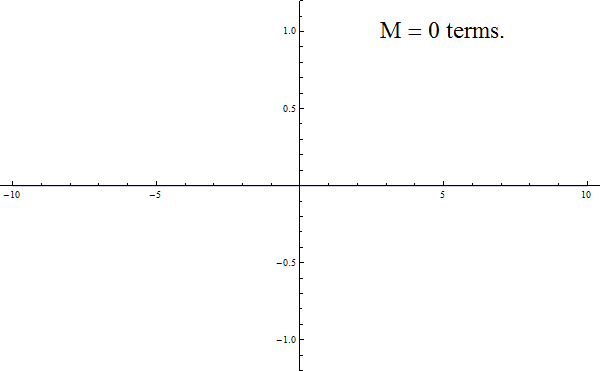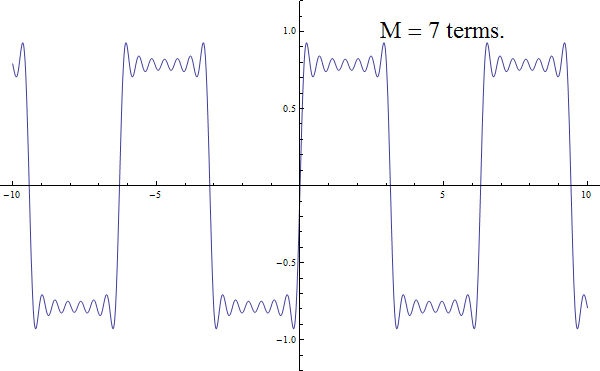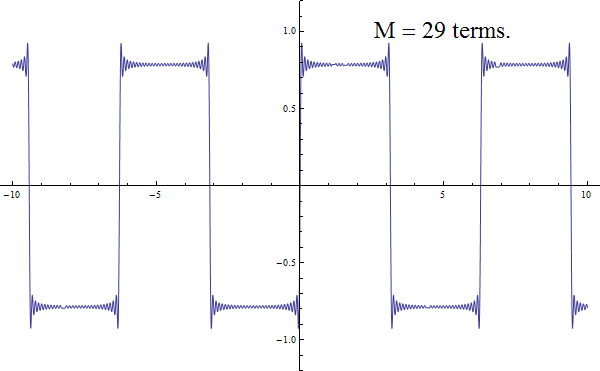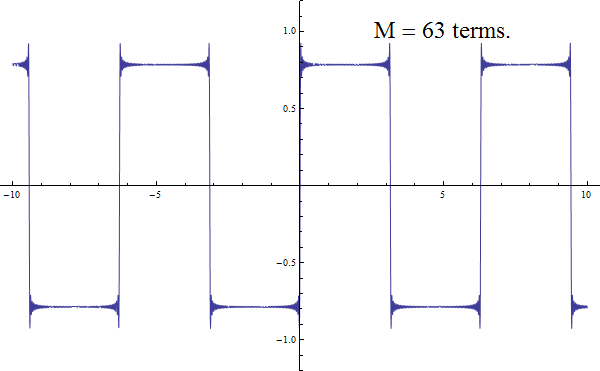Interestingly, the first article on cp4space was concerned with Fourier series and pathological functions. Assuming you haven’t read it (which is plausible, since it precluded the early-2013 popularity surge), I suppose I should start by re-introducing them.
Fourier reasoned that periodic functions such as the sound waves produced by musical instruments could be expressed as superpositions of simple sinusoidal waves of different frequencies. As a basic example, successive approximations to the square wave are summarised in this animated GIF:
As a slight aside, I’m always slightly wary about including animated GIFs in my articles, since the last one ended up on the website Tumblr (home to such delights as Sherlock Holmes doffing his scarf) and featuring some rather interesting tags:
What if we want to perform a similar treatment to aperiodic functions? It transpires that it is possible, as long as we allow a continuum of frequencies instead of a discrete series. In this case, the summation is replaced with integration, and we obtain the beautiful Fourier transform:
The inverse Fourier transform is obtained by deleting the minus sign in the above expression. Interestingly, the four-fold composition of the Fourier transform operator is the identity (F^^^^ = F), which led people to consider the concept of a fractional Fourier transform by an arbitrary angle (where the original Fourier transform operator corresponds to a 90° rotation in time-frequency space), a useful tool for noise reduction in signal processing.
Anyway, the Fourier transform has some nice properties. For instance, if we view functions from 
Discrete Fourier transform
Since we’re now living in a finite-dimensional vector space 
We also have the beautiful relationship between pointwise multiplication and sequence convolution of vectors:
-
DFT(x convolve y) = DFT(x) pointwise DFT(y)
This will become useful later. Note also that there is nothing special about the complex numbers in this context, and we can replace them with another ring (such as modular arithmetic). If we do so, we obtain the number-theoretic tranform (NTT), which has the nice property that it can be implemented on a computer with exact integer arithmetic instead of all of that tedious fiddling around with complex numbers.
Now, convolution is a rather common operation, which is used (amongst other things) for multiplying two polynomials:
(a0 + a1 X + a2 X^2 + …)(b0 + b1 X + b2 X^2 + …) = (a0 b0 + (a1 b0 + a0 b1) X + (a2 b0 + a1 b1 + a0 b2) X^2 + …)
Strictly speaking, the convolution in the context of the discrete Fourier transform is cyclic convolution, since the sequences ‘wrap around’. However, this only produces minor annoyances that do not affect the asymptotic analysis of…
…the Schönhage-Strassen algorithm
Basically, the ordinary algorithm for multiplying integers treats them as polynomials in some number (the base) and convolves them. But using the number-theoretic transform, we can reduce convolution (the expensive task) to pointwise multiplication, which in turn can be performed recursively using this algorithm. If we carefully choose the base at each stage (say by chopping the original N-bit numbers into about sqrt(N) blocks), then we get a recursion depth of log log N and an asymptotic running time of O(N log N log log N).
A slightly more sophisticated variant, Fürer’s algorithm, reduces the running time even further to O(N log N 2^log*(N)), where log* is the iterated logarithm function. However, for all practical applications, it is faster to use Schönhage-Strassen (with Fürer only overtaking for astronomically huge numbers).
Wait… did I say practical applications?
Surprisingly, multiplying huge numbers does indeed have its advantages. Although the numbers used in RSA cryptography are sufficiently small that the Karatsuba multiplication algorithm is better, testing Mersenne primes using the Lucas-Lehmer test requires multiplying integers with millions of digits (safely within the realm of optimality of Schönhage-Strassen).