If I have seen further it is by standing on the shoulders of giants.
This memorable quotation from Sir Isaac Newton, it has been speculated, was a subtle derogatory reference to the physical stature of his rival, Robert Hooke. Many derivative quotations have emerged from it, my favourite being this intensely humorous one of Hal Abelson:
If I have not seen as far as others, it is because there were giants standing on my shoulders.
Anyway, one of the more ubiquitous immortalisations of the original quotation is on the milled edge of a two-pound coin, which bears the inscription ‘standing on the shoulders of giants’. Incidentally, the milled edge was itself an invention of the same Sir Isaac Newton, which he incorporated into coins whilst Warden of the Royal Mint to prevent the entirely dishonourable practice of ‘clipping’, where fruadulent scoundrels would shave off a thin layer of gold from coins.
The innermost annulus, surrounding a chariot wheel and bounded by a design reminiscent of a printed circuit board, features a ring of interlocking gears of various types, all of which mesh together. Do you notice anything bizarre about them?
A quick enumeration confirms that there are precisely nineteen gears in this closed loop. If you were to rotate them, adjacent gears would turn in opposite directions, which is of course impossible for an odd number of gears in a planar loop. Several people complained about this, for instance here.
At the Archimedeans’ annual dinner, Joseph Myers happened to mention in passing that this ‘would not work unless the gears were arranged in a Möbius strip’. If they were, then an odd number of gears is actually required: the lack of orientability means that a clockwise-rotating gear becomes an anticlockwise-rotating gear when moved around the strip, and we can indeed have nineteen perfectly rotating gears. Conveniently, I still have the gear-drawing code from my Antikythera mechanism, so we can see nineteen interlocking gears in action:
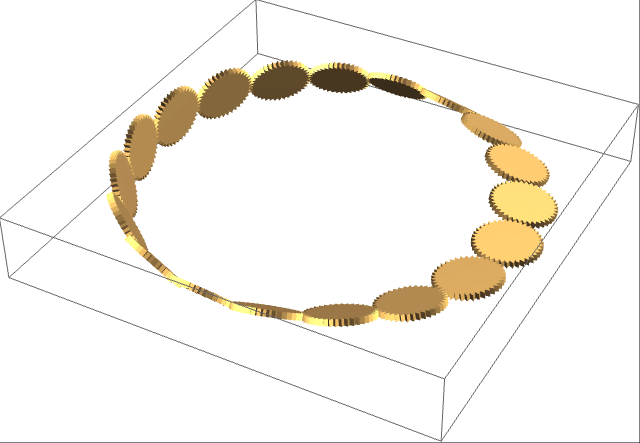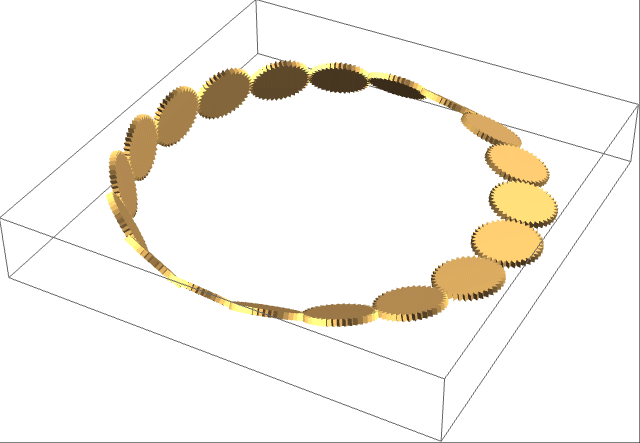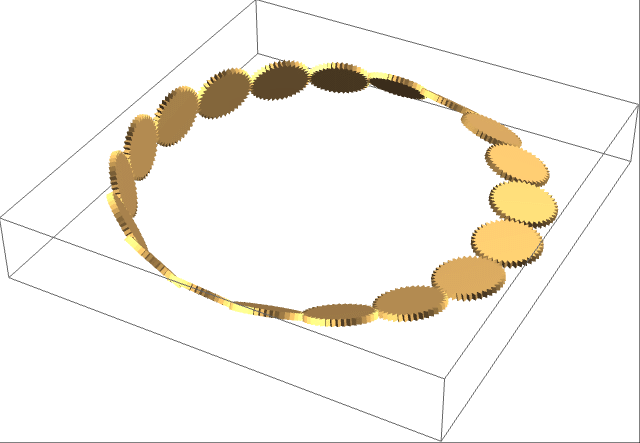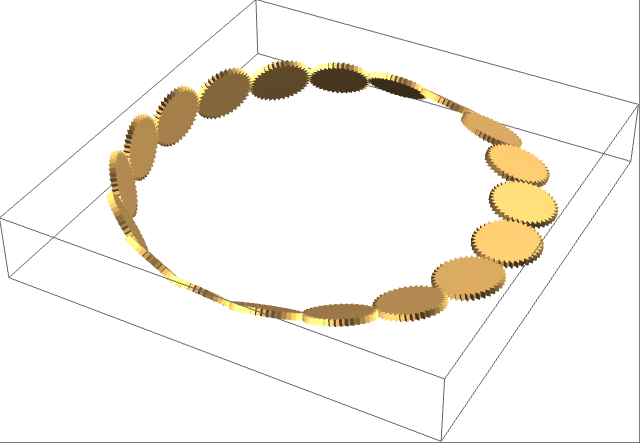
Michael Trott has gone two steps further. Firstly, he noticed that the gear chain can double-cover a Möbius strip such that the gears are Hopf-linked together to form the first iteration of Antoine’s necklace:
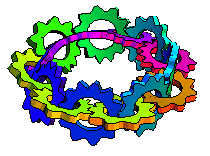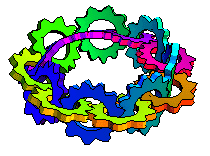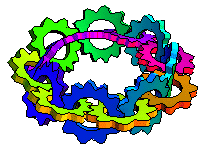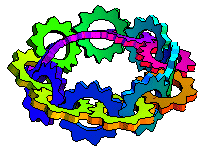
Secondly, Trott proceeded to bend the resulting chain into a trefoil knot:

Earliest examples of gears?
Intricate mechanical gears have existed since antiquity and beyond. I already mentioned the Antikythera mechanism, which astounded archaeologists by predating any other known machines of that complexity by several centuries. An earlier example of gears is the Chinese south-pointing chariot, which uses a simple system of cogs to ensure that a pointer continually points south, even as the chariot itself turns. This facilitated navigation before the magnetic compass had been developed.
However, researchers at the Department of Zoology (University of Cambridge) recently discovered that the leaf-hopping insect Issus has a pair of interlocking gears used to synchronise leg motions to within 30 microseconds of each other, far beyond what is achievable by the nervous system. This, of course, is profoundly older than either the Antikythera mechanism or the south-pointing chariot, although admittedly far simpler than either.
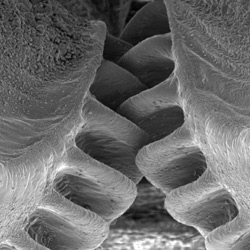
Somewhat curiously, the gears are only present in the juvenile Issus, rather than its adult form.


I don’t recall making that comment, and you were at the next table with Béla Bollobás and Sreya Saha for most of the dinner, a bit far to talk….
Yes, I have total recollection of dining betwixt the aforementioned awesome people, although I can equally well remember you making such a comment. At least, I’m moderately sure it was you. Maybe I dreamt it…
“This memorable quotation from Sir Isaac Newton”…
Standing on the shoulders of giants… is not Newton’s original thought… it is only a paraphrase of much older source/sources… from Medieval period or even earlier from ancient Greece
http://en.wikipedia.org/wiki/Standing_on_the_shoulders_of_giants
Pingback: Denser packing of pound coins discovered | Complex Projective 4-Space