Neil Bickford has exhaustively searched the space of 5 × 4 sliding-block puzzles* to determine the one with the longest minimal solution. The unique result, which requires a whopping 235 moves, happens to be Bob Henderson’s Gauntlet puzzle:
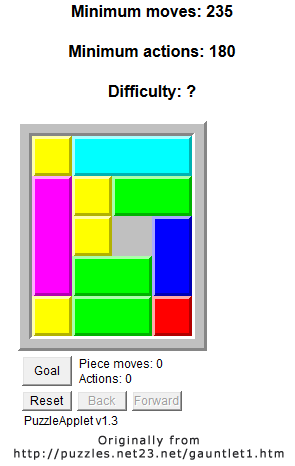
*subject to the constraint that the objective is to move the red monomino to the upper-left corner.
Despite having far fewer positions than a Rubik’s cube, the graph of this sliding-block puzzle has a much longer diameter. Tomas Rokicki proved that the Rubik’s cube has a diameter of 20 in the half-turn metric, and there’s an upper bound of 28 for its diameter in the more natural quarter-turn metric. It has also recently been proved that the Rubik’s cube Cayley graph (which is vertex- and edge-transitive) is also Hamiltonian; it is conjectured that every Cayley graph is Hamiltonian.
Now, chess problems are harder than sliding-block puzzles, since you have to account for all possible moves that your opponent could make. For instance, ‘mate in 3’ problems are quite difficult due to the plethora of possible combinations for which one must account. This is reflected in the fact that (generalised) chess is EXPTIME-complete, whereas sliding-block puzzles are merely PSPACE-complete.
If mate-in-3 problems can be difficult, then surely the following mate-in-549 problem must be completely intractable? Even the best grandmasters can see no logic behind the majority of the moves, since the depth of the problem is beyond human comprehension. Indeed, it would probably please even Doron Zeilberger, who considers Fermat’s Last Theorem to be trivial due to the existence of a human proof.

White to play and mate in 549…
This configuration was discovered by programmers at Lomonosov University, Moscow, who exhaustively catalogued all reasonable seven-piece chess endgames. White can force a win, eventually, but Black can prolong defeat for as many as 549 moves. Interestingly, the optimal sequence of moves for White involves promoting the pawn to a knight, rather than to a queen.
If we’re allowed an infinite board, then it’s possible to have mate-in-ω games and beyond, where White eventually wins, but Black can delay White by an arbitrarily long time. It is also conceivable that there is an algorithm for converting a statement in Peano arithmetic to a chess configuration in which White can force a checkmate if and only if the statement is true. (Both of these rely on the fact that rooks, bishops and queens can move by any integer in a single move.)

Has there been any analysis of problems on an infinite (or just larger) board where some or all of those pieces have maximum distances per move? Note that as long as those maxima are all at least seven squares per move then it’s still an extension of normal chess, as the board size of normal chess prevents longer moves than that anyway.
Bounding the distances immediately removes the `checkmate in omega moves’ possibility, since there are only finitely many possible moves at each step, so by König’s tree lemma every winning position is a `mate-in-n’ for some positive integer n. Hence, the game becomes less interesting than in the unbounded move case. In particular, only Pi^0_1 problems — equivalent to the Halting Problem — can be encoded, rather than arbitrary arithmetical problems.
I wonder if this configuration is achievable from usual starting position. From what I know, deciding if a configuration A can be reached from configuration B is, in general, EXPTIME-complete, so it suggests that it might be possible for this configuration to be unreachable.
No, it can be at most PSPACE-complete to determine whether a given position can be reached. I’m pretty sure that one could easily contrive a sequence of moves culminating in that 549-move endgame; I’ll leave it as an exercise for the reader.
Reblogged this on Chess Musings and commented:
Mate in 549! A little about the world’s most difficult chess problem, math and programming.
Pingback: Daily Chess News Links March 30, 2014 | blog.chesscafe.com
I’m not sure that ‘length of minimal solution path’ is a good measure of difficulty for sliding-block puzzles of this form.
I once wrote a program to randomly generate puzzles of that type for my puzzle collection (but sadly it turned out a bit too slow to be sensibly usable) and tried playing a few with various settings. I found that if I insisted that the program find a long minimal solution, it often tended to be achieved at the expense of difficulty, in the sense that at most steps there was only one move that could possibly make sense, so it was a no-brainer to just make that move. In puzzles with a shorter solution path, it seemed much more common to find a great deal more branching, so that you’d constantly be presented with several next moves that plausibly might be fruitful and it wouldn’t be immediately obvious which one was actually fruitful.
Of course that might just have been some sort of artefact of my random-generation technique (which was basically to fill the grid with monominoes, then repeatedly join together two adjacent pieces into a larger piece as long as doing so did not prevent my BFS solver from finding a solution) and not a characteristic of all possible instances of this puzzle type. But then, it might not.
Thanks for your thoughtful comment, Simon. I will admit that the main reason the “length of minimal solution” metric is used is because it is easiest to verify using computer solvers (and easiest to generate by running a solver in reverse from a complete set of winning positions). In its defense, a long “narrow” solution can still be quite difficult for a human to solve, since there is seldom an obvious choice as to which move will get you closer to the goal (even though the number of such decision points may be relatively small).
It’s sometimes informative to look at the tree of possible positions as a graph. Here’s the graph for the hardest 4-by-4 simple^3 problem:
http://cp4space.files.wordpress.com/2013/06/sbp-graph.png
It is interesting how we get several large islands, adjacent pairs of which are joined by a narrow isthmus.
Nice visualization! I had imagined that slide puzzle position graph topology was similar to that of a tattered fishing net, but the one above appears to be down to its last few strands before disintegrating! It also seems to exhibit something close to up-down symmetry. I would expect such a symmetry if the puzzle had only rectangular pieces: the same pieces would end up in the same orientations after the whole puzzle was rotated 180 degrees clockwise. Parity issues could also divide the position graph into disconnected pieces for slide puzzles having only one empty space, such as those in my “Gauntlet” series.
I had always wondered about this problem [both the sliding block and the chess problems]… Nice to see someone spent time analyzing the problem. It’s one less thing that I have to look at. Excellent job to everyone involved.
Thanks for the mention — I had no idea that any of my puzzles were that well known, much less that I am remembered as their source! There’s just one fly in the ointment — my file copy of the 5 by 4 “Gauntlet” puzzle dated Aug. 17, 2002 requires 243 moves rather than 235 moves (it also has 6 dominoes and 7 monominoes rather than 2 trominoes, 4 dominoes and 5 monominoes). You might want to download Rodolfo Valeiras’ “Deslizzzp” puzzle game to see and/or play it yourself. I am guessing that Neil Bickford made some assumption that the 243-move version violates.
Neil Bickford decided to restrict his search to what he deems `simple^3′ problems. According to his blog post, “it means that each piece is different from another only by its shape [except for the red piece], and that the goal is to get the top-left-most [red] piece down to the lower-right”.
Personally I prefer the style of puzzle “get from configuration A to configuration B, where pieces are distinguished only by their shape”, as it seems to be more natural.
True, that is a perfectly natural slide puzzle definition which leads to the concept of the puzzle diameter (the most moves from one position to any other). As Nick Baxter notes at his Sliding Block Puzzle site, “one piece to one board position” is probably an easier goal to grasp, since the solver can see just how far the object piece has to move to get to its goal position. . . If only all the other pieces weren’t so obstinately blocking the path!
Did Neil assume that the red monomino starts in the opposite corner from its goal position?
Yes.
The Sliding Block Puzzle is commonly known as klotski.
Would Neil be interested in discussing his research program? Several years ago I ran analyses of 4×5 and even 5×5 slide puzzles for a range of different goal descriptions and piece types. Only a few of the better results have been shown at Dries de Clerq’s and Nick Baxter’s sliding puzzle sites.
Pingback: Mueven blancas y mate en 549 | Misiongeek
Pingback: Mueven blancas y mate en 549 | recolector.de {tecnologia}
Pingback: Juegan blancas y mate en 549 | recolector.de {tecnologia}
Pingback: Juegan blancas y mate en 549 | SUNETFON
Are there any results concerning hard mate-in-n problems where the mate is actually playable in a game? This mate-in-549 fails, since after 50 consecutive moves with no captures or pawn moves (which must occur, since there are so few pieces) the game would be declared a draw.
Pretty! This was an extremely wonderful post. Thank you for providing this info.
SPAM SPAM SPAM SPAM
Perhaps this is not really relevant but the chess position shown is incorrect. The white queen should be g7 instead of f7 for there to be mate in 549. The position shown is a draw.
Thank you — fixed!