Cayley-Menger determinants

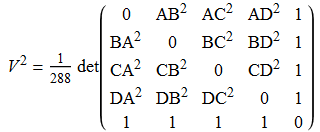
Niccolo Fontana Tartaglia, whom you may recognise from having discovered Cardano’s solution to the general cubic equation, also discovered a generalisation of Heron’s formula to compute the volume of a tetrahedron:

As you may expect, this can be generalised to compute the volume of any n-simplex (n = 2 reducing to Heron’s formula for the area of a triangle). I wondered how one would go about proving this identity, and then realised it can be accomplished by elementary facts about determinants. Firstly, it is easy to show the following result:

• The volume of an n-simplex S with vertices at {0, e_1, …, e_n} is equal to 1/n!, where e_i is the ith standard basis vector.

This can be proved, for instance, by subdividing a unit cube into n! simplices, each of which is congruent to S. Now, we know that the determinant of a matrix gives the volume scale factor of the associated linear transformation, enabling us to generalise the previous result:

• The volume of an n-simplex T with vertices at {0, a_1, …, a_n} is equal to V = det(a_1, …, a_n)/n! where we form the matrix by writing down the coordinates of a_i in the ith column.

Recall that determinants are multiplicative, so we can multiply this by its transpose to get the following equation (which is satisfyingly coordinate-independent):

• V² = (det R)/((n!)²), where the entries of R are given by Rij = a_i · a_j.

And then by scaling, we obtain:

• V² = (det Q)/((−2)^n (n!)²), where the entries of Q are given by Qij = −2 a_i · a_j.

This in turn leads to the following:

• V² = (det P)/((−2)^(n+1) (n!)²), where P (an n + 2 by n + 2 matrix) is obtained by taking the matrix Q and appending two useless ‘1’s (whose only affect is to negate the determinant) to the diagonal like so:

Now, we want to apply determinant-preserving elementary row operations to convert the Cayley-Menger matrix M given at the beginning of the article into the matrix P. Perform the following operations in succession:

• Subtract the 1st row from the 2nd, 3rd, …, (n+1)th rows;
• Subtract appropriate multiples of the final column from the other columns so that the first row is (0, 0, 0, …, 0, 1);
• Subtract the 1st column from the 2nd, 3rd, …, (n+1)th columns;
• Subtract appropriate multiples of the final row from the other rows so that the first column is (0, 0, 0, …, 0, 1).

Then it is easy to verify that the result is equal to P, by expanding each entry in terms of dot products.

Applications of the Cayley-Menger determinant

• The Cayley-Menger determinant is beautiful in its own right, expressing the squared volume of a tetrahedron solely as a polynomial in the squared edge lengths. Similar results hold for other polyhedra, which was a necessary component in establishing the Bellows Conjecture.
• If we form the Cayley-Menger determinant of five nearby points in general linear position in three-dimensional space, it will allow one to deduce whether the local Gaussian curvature is positive, zero or negative. This is described in more detail here.
• Several other theorems in distance geometry follow as special cases, such as Stewart’s theorem.
• The distances between atoms are determined by the bond lengths, so the shapes of certain molecules can be predicted using distance geometry.