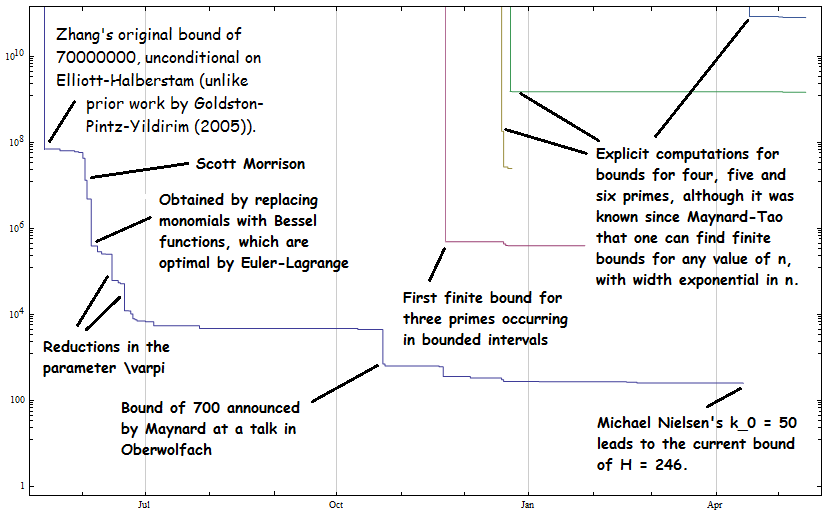
It’s been just over a year since Zhang’s seminal proof that there exist infinitely many pairs of primes separated by a distance at most H = 70000000. There have been many advancements since then, and the current status is a bound of H = 246:
If we assume the Elliott-Halberstam conjecture, then we obtain the much improved value of k0 = 3, corresponding to a bound of H = 6 given by the following admissible 3-tuple:
* _ _ _ * _ *
Consequently, assuming Elliott-Halberstam, there are either infinitely many pairs of twin primes, cousin primes or sexy primes. (Most probably, there are infinitely many pairs of each.)
Other Polymath projects
The bounded gaps effort is not the only massively collaborative mathematical project in recent history, although it is probably the best known. Some of the others are summarised below:
-
Polymath1: This project successfully resulted in a combinatorial proof of the Density Hales-Jewett theorem of Ramsey theory, giving results such as Szemeredi’s theorem for free. This provides improved bounds and is more elementary than the earlier proofs using ergodic theory.
- Polymath4: Is there a deterministic algorithm to find a prime of at least N digits in time polynomial in N? Obviously, there are probabilistic algorithms, such as randomly choosing primes and applying the AKS primality test until we obtain a positive result. A deterministic algorithm would also result from the truth of Cramér’s conjecture.
- Polymath5: The Erdös discrepancy conjecture claims that if we have an infinite sequence where each term is +1 or −1, then we can find arithmetic progressions of the form {d, 2d, 3d, …, kd} whose sum has arbitrarily large absolute value. (Note that anchoring the AP at zero is necessary; otherwise, this would be a trivial corollary of van der Waerden’s theorem, which in turn follows from Polymath1.) Using a SAT solver, it was proved that every sequence of length 1161 or longer must have a zero-anchored arithmetic progression with a sum of ±3.
- Polymath7: The Hot Spots Conjecture states that if we have a non-uniformly heated compact sheet of metal and allow the heat to diffuse, then there will be a time beyond which the hottest point lies on the boundary of the sheet. It has been refuted for certain domains, and proved in others (such as obtuse- and right-angled triangles). This project attempts to prove the conjecture for acute-angled triangles.
For more information, consult Michael Nielsen’s website.