Disclaimer (mainly to Marcus du Sautoy): The Ancient Greeks did not invent integration, and whilst I shall use Ancient Greek principles of mensuration to justify Riemann and Lebesgue integration, the Ancient Greeks did no such thing.
Finding volumes of cones and spheres
So, suppose you want to calculate the volume of a sphere, and hitherto only know that the volume of a cylinder is πr²h. We cannot use a clever argument involving cutting the cylinder into finitely many compact pieces with piecewise-smooth boundaries and reassembling them into a sphere, as you can convince yourself that the quantity:
I = total area of convex spherical surface − total area of concave spherical surface
must remain invariant under the operations of dissecting and reassembling. And since a cylinder has I = 0 whereas a sphere has I > 0, they are not scissors-congruent.
A more powerful idea is Cavalieri’s principle, which states that if every horizontal plane through two bodies A and B intersects them to give cross-sections of equal area, then A and B have the same volume. We can use this to deduce that a cone and pyramid of the same base area and height have the same volume. We can also deduce that a cylinder and square-based prism of the same cross-sectional area and height have the same volume.
Then, using a dissection argument, we can show that a pyramid has one third of the volume of its bounding cuboid. Putting these three facts together leads to a simple relationship between the volumes of a cone and cylinder of the same base area and height:
In other words, a cone has volume πr²h/3.
The next part is a significantly more sophisticated application of Cavalieri. Suppose we have a sphere of radius R centred on the origin, and consider the intersection with the horizontal plane z = a. By Pythagoras’ theorem, this has area r² − a², which is coincidentally also the area of an annulus bounded between concentric circles of radii r and a. Consequently, we can apply Cavalieri’s principle to show that a sphere has the same volume as the solid obtained by removing a double-cone from a cylinder:
Now, the cylinder has volume 2πr³ and double-cone has volume 2πr³/3, so the sphere must have volume equal to their difference, 4πr³/3.
Riemann versus Lebesgue integration
When Archimedes calculated upper and lower bounds for the value of π, he did so by bounding a circle between a circumscribed and inscribed 96-gon. By increasing the number of sides of the polygons, we can obtain tighter bounds.
If the supremum of the lower bounds agrees with the infimum of the upper bounds (which it does for these regular polygonal approximations), then we have the exact area of the circle. Riemann integration uses precisely this method of exhaustion to find the area under general curves.
Unfortunately, not all functions are Riemann-integrable. The standard counter-example is the function defined on [0, 1] by f(x) = 1 if x is rational, and f(x) = 0 otherwise. The infimum of the upper bounds is 1, whereas the supremum of the lower bounds is 0, so we cannot obtain a precise value of the integral.
We can, however, use Cavalieri’s principle to produce a function g with the same area as f, but such that g is Riemann-integrable. In particular, for a general measurable function f, take g to be as follows:
g(x) = supremum of y such that {z | f(z) ≤ y} has Lebesgue measure ≥ x.
Then f and g are Cavalieri-equivalent on a co-countable (untable?) set of values of y, so f and g must have the same area. But g is a monotonically decreasing function, so is therefore integrable. This gives the Lebesgue integral of f. In the case of the indicator function of the rationals, the Lebesgue integral is 0.


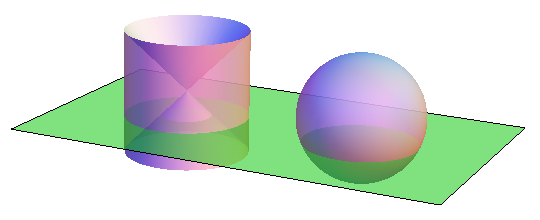

Missing a factor of pi in the areas mentioned during the second application of Cavalieri.
sphere + cone = cylinder:
http://blog.zacharyabel.com/wp-content/uploads/2012/01/stab-hemisphere.gif
*hemisphere + cone = cylinder
Cute animation, nonetheless. 🙂