Quaternions were discovered by Sir William Rowan Hamilton in a flash of inspiration as he crossed Brougham Bridge, inscribing the following relations into one of the stones:
i² = j² = k² = ijk = −1
Specifically, a quaternion is a number of the form q = a + bi + cj + dk, where a, b, c, and d are real and the elements i, j and k satisfy the above relations.
Note that multiplication of quaternions is non-commutative, but the other field axioms hold as expected. In particular, addition forms an Abelian group, multiplication is associative and distributes over addition, and we have a multiplicative identity, 1. Moreover, the real line occurs as a subspace of the quaternions; this is precisely the centre of the multiplicative group.
The notions of ‘absolute value’ and ‘complex conjugation’ generalise to quaternions in the obvious way. Specifically, the multiplicative inverse of q is given by:
q^-1 = q*/|q|² = (a − bi − cj − dk)/(a² + b² + c² + d²)
Also, note that if q is a non-real quaternion, the R-linear subspace spanned by 1 and q is isomorphic to the field of complex numbers.
Rotations in  and
and 
In two dimensions, a general rotation can be expressed in the form z → az, where a is a complex number of unit norm. One may naïvely assume that the same result holds for quaternions. However, this is untrue: we require a pair of unit quaternions, (a, b), to represent a general rotation q → aqb*. Moreover, (a, b) and (-a, –b) represent the same rotation, so S³ × S³ is isomorphic to Spin(4), the double-cover of SO(4).
The diagonal subgroup {(a, a) : a in S³} has the property of fixing all points on the real line. Consequently, the three-space spanned by {i, j, k} is preserved by this subgroup, so we can represent three-dimensional rotations by unit quaternions. Indeed, S³ is isomorphic to Spin(3), the double-cover of SO(3).
Question 3 of NST1 2011
The following question appeared on a selection test for the British IMO team:
See if you can solve it (solutions are welcome in the comments at the foot of this page).

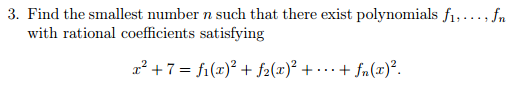
If “rational coefficients” allows complex ones with rational components, then n = 3; f1(x) = x, f2(x) = 4, f3(x) = 3i. Otherwise, it looks like n is at most 5: f1(x) = x, f2(x) = 2, f3(x) = f4(x) = f5(x) = 1.
Note that the x^2 seems to have to come from a bare x as one of the polynomials; if f_k(x) was ax + b, it would contribute a^2x^2 + 2abx + b^2 and we’d have to get rid of the 2abx somehow. The only way is with more polynomials with the same structure, ending up with sum(a_k^2) = 1, sum(a_kb_k) = 0, and (if we want no other fs) sum(b_k^2) = 7. The latter requires an integer solution to sum(x_k^2) = 7y^2, though (where y is a common multiple of the denominators of the b_k, and the x_k are the b_k times y are integers). That’s impossible, for n < 4 though. If y is written as s*2^r where s is odd, y^2 = s^2*4^r, and s^2 is congruent to 1 mod 8, so 7s^2 is congruent to 7 mod 8 and 7y^2 runs afoul of Legendre's Three Square Theorem, excluding n = 3; 7 being not a square excludes n = 1 and 7 being congruent to 3 mod 4 excludes n = 2.
For n = 4 it seems like it *should* be possible. We need a, b, c, d whose squares sum to 1 and e, f, g, h whose squares sum to 7, with the property that ae + bf + cg + dh = 0. This turns out to be equivalent to finding a, b, c, d whose squares sum to a perfect square and e, f, g, h whose squares sum to 7 times a perfect square, in integers, with the same constraint ae + bf + cg + dh = 0.
Conjugacy considerations (mainly mod 4) indicate that for a primitive solution (a, b, c, d lack a common factor and e, f, g, h lack a common factor), a, b, c, d are either all odd or three even, one odd, and e, f, g, h are either all odd or one even, three odd. This does not seem to preclude a solution existing. I have not been able to find a solution in small integers to this, however.
So, n may be 4 and is definitely either 4 or 5.
I think I now have a proof that n must be 5. If n were 4, we could take the coefficients of x from our polynomials and make of them a unit quaternion w with rational coordinates. The coefficients of 1 would form a quaternion z with norm sqrt(7). The ae + bf + cg + dh = 0 criterion amounts to “wz is pure imaginary”. But wz also has norm sqrt(7), so we’d need to have the sum of three squares, the imaginary-component magnitudes of wz, adding to 7, which is impossible by Legendre’s Three Square Theorem.
So n = 5, and x, 2, 1, 1, 1 is a minimal solution (though not unique; there’s also x, 3/2, 3/2, 3/2, 1/2; x, 9/5, 7/5, 6/5, 3/5; x, 2, 5/3, 1/3, 1/3; x, 5/3, 5/3, 1, 2/3; x, 13/5, 2/5, 1/5, 1/5; x, 5/2, 1/2, 1/2, 1/2; x, 2, 7/5, 1, 1/5; and, it seems likely, infinitely many more like this, as well as ones with more interesting degree-1 polynomials than just a bare number or x).
Well done! I think that your proof may be even neater than my (similarly quaternionic, and probably equivalent) proof, which was:
“Let (w, z) be a solution (using your notation). The necessary and sufficient conditions are that |w|^2 = 1, |z|^2 = 7, and w . z = 0 (in the Euclidean inner product). Hence we can premultiply w and z by w* to give another solution (ww*, zw*). But ww* is purely real, so zw* is purely imaginary. Contradiction.”
However, my proof does provide a way to generate an infinite family (and possibly all) solutions — just `rotate’ your initial solution (w, z) by any pair of unit quaternions with rational coefficients. And we can enumerate all of *those* by the same `inversion’ technique for enumerating Pythagorean triples, but in R^4 instead of R^2..
First a clarification: ae + bf + cg + dh = 0 amounts to “wz is pure imaginary” since we can flip the signs of f, g, and h say, without altering the sums of squares, and get ae – bf – cg – dh. So given any solution you’d be able to derive from it a pair of quaternions w and z with the requisite property.
Second, if this is generalized to x^2 + m for some positive integer m, it seems that n is 5 if m runs afoul of Legendre’s Three Square Theorem, but is never higher (since all positive integers are sums of four squares, one can always find an x, a, b, c, d solution for any positive integer m); if m divided by its highest internal power of four is not congruent to 7 mod 8, n is at most 4. n = 1 for only m = 0 and n = 2 if k is a perfect square — even if we have general ax + b and cx + d, to get (a^2 + c^2)x = x, a^2 and c^2 end up being p/r and q/r where p, q, r form a Pythagorean triplet, b:d = – c:a, so there is some s such that c = -bs and d = as, and thence b^2 + d^2 = r^2s^2 = m is a perfect square. If m is a non-square sum of two squares, then obviously n = 3, and the question that remains is if the set of m for which n = 3 is precisely that or is some larger subset of non-Legendre-affected m. Now, consider the quaternions again, with |z| = 1, |w|^2 = m, wz pure imaginary, and w’s and z’s fourth components equal to zero, so z = a + bi + cj and w = e + fi + gj. In that case, wz being pure imaginary may still have three nonzero components, as for example the expansion for zw includes a term bgk that need not be zero. So if m is non-Legendre-affected this and the underconstrained nature of the system otherwise (six unknowns in three equations!) strongly hints that there will be solutions with n = 3. So n = 4 *may* not occur for any m … though, I don’t know for sure.
What makes it difficult is the lack of a three-dimensional normed division algebra. This is what Hamilton was seeking before he found the quaternions, I seem to recall.
I conjecture that n = 4 in the case of m = 3, mainly because my attempts to find a solution for three polynomials failed.
Sorry, what was I thinking? *Obviously* x^2 + 3 requires four polynomials; just substitute x = 2 and appeal to Legendre!
Yeah, that works. So n = 4 does occur, for (at least) the subset of m where m itself doesn’t run afoul of Legendre, but there exists some integer s with s^2 + m doing so. This is some subset of the m for which m is a sum of three squares, since if m is a sum of two squares, s^2 + m cannot run into Legendre and besides we have the n = 3 solution [x, square 1, square 2].
Actually, it looks likely to be *all* the m that are sums of three squares but not of fewer that have n = 4. If every sum of three squares occurs as three of the four squares adding up to some Legendre-number, then that will be the case. Only if there is some a^2 + b^2 + c^2 with the property that for *all* integers d, a^2 + b^2 + c^2 + d^2 can be rewritten as e^2 + f^2 + g^2 (in integers!), might we have an instance where m is a three-square number but n = 3.
Congruency considerations narrow down when that might happen. The residues mod 8 are 0, 1, and 4; the possible signatures of our triplet with respect to this (up to rearrangement) are [0 0 0], [0 0 1], [0 0 4], [0 1 1], [0 1 4], [0 4 4], [1 1 1], [1 1 4], [1 4 4], [4 4 4]. Of these:
[0 0 0], [0 4 4] are divisible by 8 and adding a d^2 with residue 4 is likely to allow getting 4*(8r + 7).
[0 0 4], [4 4 4] are odd multiples of 4 and adding a d^2 with residue 0 is likely to allow getting 4*(8r + 7).
[1 1 1] is congruent to 3 mod 8; just add a d^2 that’s an odd multiple of 4 (such as, say, 4) and the result is odd and congruent to 7 mod 8. Adding a d^2 that’s odd would produce an odd multiple of 4, and is likely to further allow getting 4*(8r + 7).
[1 1 4] is congruent to 6 mod 8; just add a d^2 that’s odd (such as, say, 1) and the result is odd and congruent to 7 mod 8.
[0 0 1], [1 4 4] are congruent to 1 mod 8.
[0 1 1] is congruent to 2 mod 8.
[0 1 4] is congruent to 5 mod 8.
So, the sums of three squares (but no fewer) that will have n = 4 are congruent to 0, 3, 4, and 6 mod 8; sums that *may* possibly have n = 3 (not ruled out yet anyway) are congruent to 1, 2, and 5 mod 8.
Of course, sums of *two* squares are [0 0], [0 1], [0 4], [1 1], [1 4], [4 4], with residues 0, 1, 2, 4, and 5, which leads to the sneaking suspicion that the sums that have n = 3 (and thus have residue sum 1, 2, or 5) are probably identical with the ones that can be re-expressed as a sum of *two* squares…
Thus, I conjecture now that for x^2 + m, n = (one more than the minimum number of squares needed to sum to m). Which has the corollary “there is always an optimal solution of the form [x, a, b, c, d] with possibly fewer constant polynomials; never does the optimal solution set contain *only* sets with a nontrivial ax + b polynomial, i.e. with neither a nor b being zero”.
(Incidentally, the above actually implies a partial *proof* of that Legendre theorem. The sums of three squares give you every residue mod 8 except 7, proving the nonexistence of three square sum forms for s = 0 in 4^s(8r + 7); when s > 0 there cannot be any 1s in the squares’ residues (as there would need to be four of them, out of a maximum of three!) so all of the squares divide by 4 and one can inductively divide all of the squared values by 2 and get a solution for 4^(s – 1)(8r + 7). The proof of existence for numbers *not* of this form proceeds, after removing powers of 4, by extending numbers congruent to 0, 3, 4, or 6 mod 8 to ones congruent to 7 mod 8 by adding a square, and then using the four square theorem; for the ones congruent to 1, 2, or 5, by finding the suspected *two* square solution and adding a 0^2 term.)
77 is a sum of three squares (8^2 + 3^2 + 2^2), but not of 2 squares (they can’t both be 72, so one is either 49 or 64, but 77 – 49 = 28 and 77 – 64 = 13), and is congruent to 5 mod 8, so any extension to a sum of four squares is congruent to 1, 5, or 6 mod 8 — while Legendre-problem numbers are all congruent to 0 or 7 mod 8. So x^2 + 77 is still a candidate for having n = 3 with no [x, constant, constant] solution in the solution set…
Ooookay, *something* screwy happened. That last one is missing a chunk of text between “be” and “72” which I definitely did not forget to include, but which disappeared somehow in transit, and is also missing its “reply” link… I *meant* to say that they can’t both be 36 or lower, as 77 is greater than 72, not that they can’t both be 72 (although they indeed can’t both be 72). And I *don’t* appreciate my comments being altered, post-“send”, by someone-or-something-other-than-me in ways that alter the meaning in a way that makes me look stupid and bad at math. I assume some dodgy automation is responsible, rather than the alteration being intentional on anyone’s part, but the effect is the same…
I think that you may have inserted the `less-than’ and `greater-than’ operators, which WordPress stupidly interpreted as being a HTML tag…
I’ve got a bit more. 77 (and also 66, and a few other numbers) run afoul of a different conjugacy “law”. The residues mod 11 are 0, 1, 3, 4, 5, and 9 — no pair of which sum to 11, other than two 0s. Thus, a sum of two squares is only ever divisible by 11 if the individual squares were both divisible by 11. From that observation, and the observation that 121 is congruent to 1 mod 8, one can infer that a number of the form 121^r*4^s*(8t + u), with neither 4 nor 121 dividing 8t + u, is not expressible as a sum of fewer than three squares if either 8t + u is divisible by 11, u = 3, u = 6, or u = 7 (and if u = 7 it requires four squares).
The necessary and sufficient condition for N to be a sum of two squares is that N = h m^2, where m is an arbitrary integer and h is not divisible by any primes of the form 4k + 3.
This eliminates the need for excessive case-bashing.