What did Alan Turing ever do for us? Answering this question is much more subtle than one would initially imagine. He has shaped the world in at least three diverse waves of influence, which despite being apparently disparate are inextricably linked both historically and mathematically.
The first of these three waves, and by far the most well-known, was his cryptanalysis of the Enigma cipher at Bletchley Park. This was pivotal in determining the outcome of the Second World War, and his contribution is considered equal to that of Winston Churchill. One can liken this accomplishment to a supernova — whilst being singularly spectacular, its effects were immediate.
The second of these waves was the development of computer science. This began in Cambridge with his seminal paper addressing the Entscheidungsproblem, and its effects today are more apparent than ever before: practically every electronic device we own is orchestrated by a variant of Turing’s idea of a universal machine. Again, this wave has recently culminated: different paradigms such as parallel computing, functional programming and even quantum computation are emerging to surpass the limitations of the Turing machine.
The third wave of influence, which is by far the least known, is still in its infancy. It began with a paper entitled The Chemical Basis of Morphogenesis, in which Turing proposed an explanation for how sophisticated patterns such as leopard spots can emerge through the processes of chemicals reacting and diffusing to adjacent cells. Here is an animation of such a reaction-diffusion system on the surface of an actual leopard in Tim Hutton’s Ready program.
Alan also investigated the phyllotaxis (arrangement of seeds) in the head of a sunflower. The number of ‘spirals’ in each direction is typically a Fibonacci number; this was recently confirmed by a Manchester-based public project, Turing’s Sunflowers. The usual model of phyllotaxis is a parametric equation for the position of the nth seed, namely . This produces a stunningly realistic and very efficient packing of seeds:

Whilst this is an incredibly accurate model of how sunflower seeds are arranged, it fails to explain why they are arranged in this manner. Obviously, the reason for doing so is to utilise the space efficiently, but the mechanism by which this is achieved is much more mysterious. After all, the process of placing seeds positioned at distances of sqrt(n) and rotated by multiples of the golden angle is not easy, especially by a plant with no internal computer!
Much more recently, an applied mathematician called Matt Pennybacker decided to investigate the partial differential equation that models the transmission of auxins (plant hormones associated with growth). He discovered that it can be idealised as follows:
Given an initial distribution of auxins on the circumference of a homogeneous disc, this partial differential equation causes an annular front to propagate towards the centre, laying down an incredibly convincing distribution of primordia:

Unlike typical reaction-diffusion systems, this involves only a single chemical u. Nevertheless, the same complexity and variety of behaviour is possible, since the underlying differential equation is fourth-order rather than second-order. These one-chemical fourth-order systems have been recently implemented in Tim Hutton’s Ready, some of which behave like the canonical two-chemical Gray-Scott model shown in the leopard animation. The result of running the sample pattern phyllotaxis_fibonacci.vti results in the following:
This is realistic near the centre, but suffers from boundary effects near the edge. The fact that this is on a square, rather than a disc, causes it to display qualitatively different behaviour from the usual sunflower. Indeed, if sunflowers were square, they would probably resemble the picture above.
Unfortunately, Turing’s untimely cyanide-induced death interrupted his fruitful investigation of biological pattern formation. Nevertheless, this year it was finally confirmed experimentally that pattern formation does indeed work in the way Turing proposed (albeit slightly refined to include heterogeneity).
At the beginning of the article, I mentioned three sequential discoveries initiated by Turing, namely mechanised cryptanalysis, computer science and pattern formation, and how the latter is still in its infancy. This suggests that there may be a fourth term in the sequence — a field that hasn’t even begun yet. A possible candidate for this is artificial intelligence; whilst some people claim that Eugene Goostman passes the test, it actually exhibits profound displays of logical inconsistency. We can, however, be certain that this article will have a sequel as soon as the next Turing-inspired breakthrough happens…
Further resources
- If you’re interested in experimenting with reaction-diffusion systems (which you should be, given that you’re reading cp4space), you can download Ready here.
- There’s a lot of really exciting stuff on Tim Hutton’s Google+ page, including more examples of partial differential equations modelling pattern formation.
- What happens when you breed white-spotted black fish with black-spotted white fish? It transpires that you actually get a labyrinthine pattern, which is the result of naively interpolating between the two reaction-diffusion equations. The results are here.


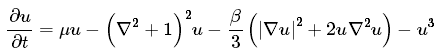

The USSR would have defeated Germany, and the US Japan, Turing or no Turing, Churchill or no Churchill – both men were almost irrelevant to the big results in WW2.