Collaborative mathematics tends to be extremely fruitful. This is epitomised by the recent ‘polymath’ projects, culminating in a nice proof of density Hales-Jewett along with the frighteningly impressive results on bounded gaps between primes. On a much smaller scale, several of us were contemplating a bunch of interesting and completely unrelated problems we devised in the downstairs kitchen of a converted house in Burrell’s Field, Trinity College, Cambridge.
We’ve made non-trivial progress on many of these, and even succeeded in solving one! It was a natural question, which grew out of a much easier problem on an IMO shortlist:
Suppose you begin with a finite graph, and are allowed to apply operations of the following form:
- Deletion: Choose a vertex of odd degree and delete it (along with all edges incident with it).
- Duplication: Produce an identical copy of the graph, and connect each vertex in the original graph to its corresponding vertex in the clone.
Show that, after finitely many operations, one can reach a graph containing no edges.
This is not terribly difficult. It did, however, lead us to consider several related questions (which, at the time of proposal, were all completely new and unsolved). Observe that neither of the allowed operations can decrease the number of connected components of the graph, so if the original graph G has n connected components, then it is impossible to end up with fewer than n vertices. This prompts the following question:
Is this bound tight? Specifically, given a graph G with n connected components, can we necessarily reduce it to the empty graph on n vertices?
It is not too difficult to show that this is equivalent to the question where n = 1. In particular, every time we perform a duplication operation, we then immediately reduce any two-vertex components to single vertices by deletion. Then we can just concentrate on each component sequentially in isolation, without undoing any of our ‘previous work’. (More formally, we can induct on the value of n.)
Hence the problem reduces to:
Can every connected graph be reduced to a single vertex?
In the next few sections, we shall present a proof in the order we devised it.
Tackling the square
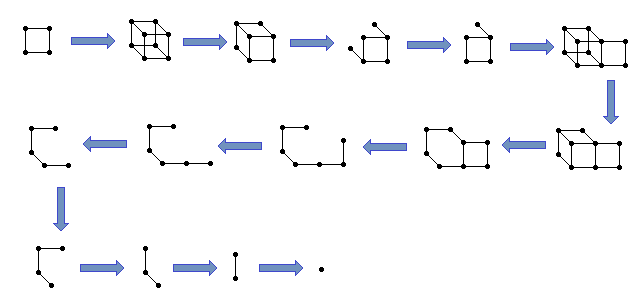
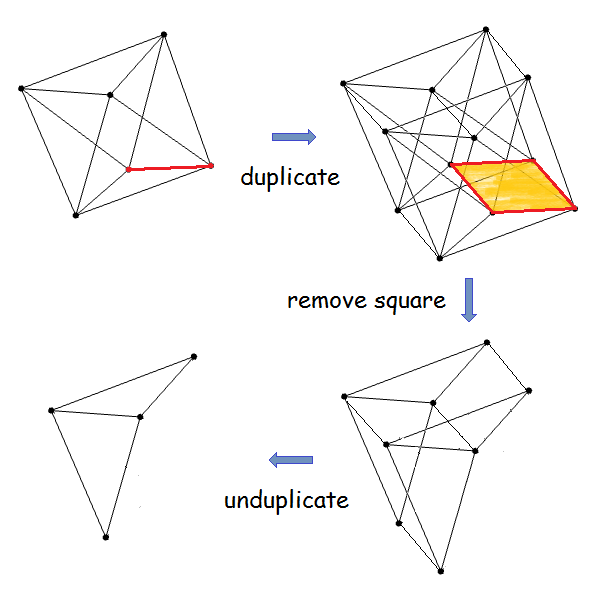
It was quite informative to consider some special cases. Any tree can quickly be destroyed by repeatedly removing leaves until we are left with a single vertex. We then decided to consider the square, since it’s the simplest graph which is not a tree (chromatic number is considered to be more important than size, since it cannot increase under either of the operations). After much experimentation, Matei Mandache found the following sequence of operations (which is provably optimal):
Using this as a lemma, we were then able to reduce any cycle, and more generally any connected graph with . This was something of a casebash, however, and clear that it would not generalise to yield a full proof. Surprisingly, this ad hoc case of reducing a square to a single vertex does turn out to be essential to our proof!
What about other graphs?
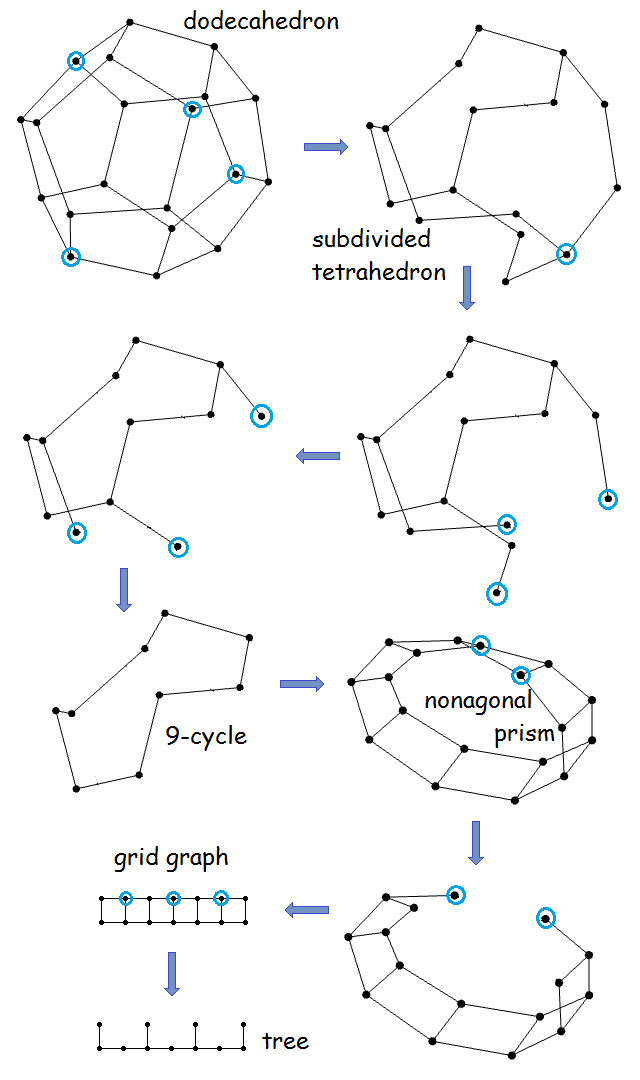
After having reduced the cube, it seemed natural to try the other Platonic solids. The tetrahedron is quite trivial (we can delete a vertex to yield a triangle, duplicate it to obtain a triangular prism, and remove two non-adjacent vertices to give a tree). The dodecahedron is slightly more convoluted, and this particular desynthesis embodies the method applicable to reducing any cycle:
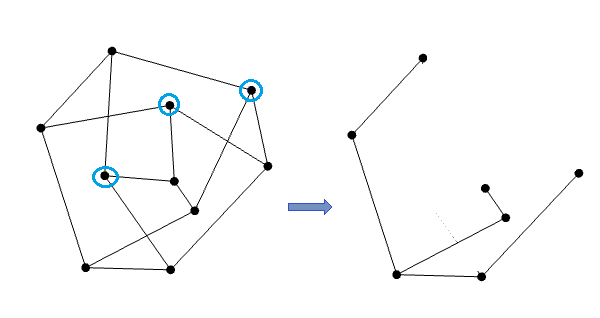
According to Donald Knuth, if a conjecture about all graphs seems plausible, it’s often the case that the Petersen graph is a counter-example. But in this case, the Petersen graph is really easy to reduce (it doesn’t require any duplication operations):
The hypercube and unduplication
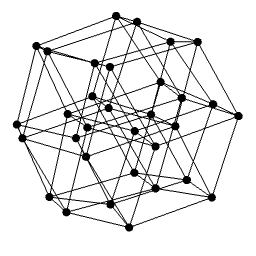
We realised that it would be very useful if we developed a method to reduce an arbitrary hypercube, since induced hypercubes appear as the result of performing repeated duplication operations. The first step in reducing a degree-(2k) hypercube must be to duplicate it to form a degree-(2k + 1) hypercube, since the former has no vertices of odd degree. Consequently, the first thing to consider was the degree-5 hypercube (with 32 vertices). Unfortunately, these things get very messy very quickly:
A more helpful way to represent this is as a ‘meta-cube’, each vertex of which is a ‘meta-vertex’ corresponding to a square of four ordinary vertices. Then we can delete an entire meta-vertex by deleting two non-adjacent vertices, followed by the other two vertices (the so-called Illingworth manoeuvre). Indeed, in any meta-graph, we can delete any meta-vertex of odd degree. And trivially we can duplicate the entire meta-graph. This has the following consequence:
The product G × C4 of a graph G with a square C4 can be reduced to a single square C4 if the graph G can be reduced to a single vertex.
And since we already know how to reduce a square to a single vertex, we obtain the following lemma:
If G can be reduced to a single vertex, then so can the product of G with a square C4.
Naturally, this can be generalised by iterated application of itself:
If G can be reduced to a single vertex, then so can the product of G with an arbitrary hypercube.
We shall think of this from an equivalent, but much more liberating, perspective:
If we grant ourselves the operation of ‘unduplication’, then the set of graphs we can reduce to a single vertex does not increase.
Henceforth, we shall thus allow unduplication.
Consequences of unduplication
Suppose we have two adjacent vertices of even degree, for example any two adjacent vertices in the octahedron. We can duplicate the graph so that these two adjacent vertices become a square of four vertices of odd degree. Then, we can remove that square by the Illingworth manoeuvre of deleting two non-adjacent vertices followed by the other two vertices. Finally, unduplicate the graph to recover the original graph minus those two vertices:
So we now have a fourth operation, namely deleting two adjacent vertices of even degree. I now claim that two of our four operations can together reduce any connected graph to a single vertex:
- Removal of a vertex of odd degree.
- Removal of two adjacent vertices of even degree.
Suppose instead that there is a counter-example, and consider a minimal counter-example (i.e. one with the fewest vertices). This must have the following properties:
- Every odd vertex is a cut-point (since otherwise we could remove that odd vertex without disconnecting the graph);
- Removing any pair of adjacent even vertices must also disconnect the graph.
Consider a graph where these properties hold. We’ll distinguish two cases, namely those where every vertex is even, and those where there exists at least one odd vertex. In each case, we shall obtain a contradiction.
Case I: At least one odd vertex exists
For each odd vertex, we can define its ‘depth’ to be the minimum order of the connected components produced when that vertex is deleted. Now take a vertex v of minimum depth; the minimal connected component produced by deleting v must necessarily consist only of even vertices (since otherwise any of those odd vertices must have lower depth). So our counter-example must resemble this:
We’ll concentrate entirely in the region on the right, where everything has even degree. Matei Mandache had the idea of separating this into strata according to their distance from v.
If the final stratum contains two vertices connected to each other, then we can delete those two adjacent vertices without disconnecting the graph. Hence, assume without loss of generality that the final stratum contains no edges.
Then every vertex in the final stratum must be connected to at least two vertices in the penultimate stratum. Consequently, we can remove one vertex in the final stratum and its neighbour in the penultimate stratum without disconnecting the graph (since everything in the final stratum is now connected to at least one vertex in the penultimate stratum).
This contradicts our assumption of minimality.
Case II: All vertices have even degree
This is actually amenable to the same proof technique as before. We let v be an arbitrary vertex, and again stratify the graph so that it resembles this:
Now we can use exactly the same proof as in the previous case.
The result follows.
What other questions can we ask?
We can ask the more general question as to whether, given graphs G and H, we can get from G to H using those two operations. Note that in general, we no longer have the freedom of unduplication or the removal of two adjacent vertices of even degree.
Clearly, we can get from G to H only if H is an induced subgraph of the product of G with a hypercube. Is the converse also true? Again, this is a strictly harder question than the one that we solved in the downstairs kitchen of ‘V’ House, but it should be quite fun to solve.
Let the collaborations begin! #oligomath


I solved the problem with a broadly similar approach (though without the concept of ‘unduplication’), but having established that I could essentially remove an odd vertex or a pair of adjacent even vertices, I finished off the proof quite differently.
Consider any connected graph G (of at least three vertices). This graph has some spanning tree, say T. Let T’ be the tree formed by removing all the leaves of T. Let u be a leaf of T’, and let v_1, v_2, …, v_n be the leaves of T that are adjacent in T to u.
Then, either some v_i is odd, in which case we can remove it, or some v_i is connected (in G) to another leaf w of T, in which case we remove v_i and w, or every v_i is connected (in G) to a vertex of T that is not one of u, v_1, …, v_n, in which case we can remove u and v_1.
Thus for every connected graph of at least three vertices, we can remove either an odd vertex or two adjacent even vertices to obtain a smaller connected graph. The result then follows as before.
When did you solve this problem?
Yes, I think that the `clever trick’ is to realise you can remove pairs of adjacent even vertices. Unduplication just makes it slightly easier to formalise.
Nice proof — I like how, unlike ours, you don’t rely on choosing a basepoint v. But then again you still choose a spanning tree arbitrarily, so maybe I’m all about that basepoint, after all.
To answer your final question, it was when I was in V-House kitchen with Matei, Sahl and Oliver. So I can bound it in the open interval (Mentoring Conference, Exit Day). Perhaps one of the others could give tighter bounds if you’re interested in establishing an order of discovery.
Those bounds are sufficient – I was chiefly interested in whether or not you had solved it before you told me about it last Sunday.
Reblogged this on Pathological Handwaving.