A while ago, I mentioned the concept of holyhedra: polyhedra, all of whose faces are multiply-connected. The first known example had 78 585 627 faces, and was later superseded by a highly symmetric example with as few as 492 faces.
Yesterday, I received an e-mail from Nathan Ho describing a 12-faced holyhedron, but it involves self-intersecting (star polygonal) faces and therefore only qualifies under a more relaxed definition of ‘polyhedron’ than the other examples:
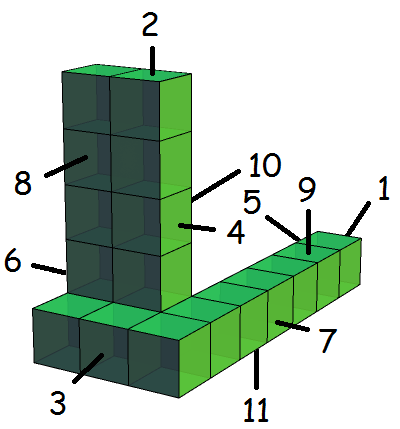
This leaves open the question of the minimum number of faces a holyhedron can possess. We know that for the deceptively similarly named golyhedra; the answer is 11 as demonstrated by Alexey Nigin’s wonderfully minimal example:
The corresponding lower bound of 11 can be derived from the following simple derivation:
- By numerical considerations, the number of faces can only be 0 or 3 (modulo 4).
- If an orthogonal polyhedron has 8 or fewer faces, then one of the three axes has at most two faces orthogonal to it. Clearly, they must point in opposite directions and have equal area, so the polyhedron cannot be a golyhedron.
Other projects
In other news, Hans Havermann has attacked the ménage prime problem with a computer search, exhausting all ménage numbers with fewer than 110 000 digits. Consequently, the expected number of ménage primes with fewer than 1000000 digits is about 0.195.
Also, I mentioned a while ago about the project to create a 31c/240 spaceship in Conway’s Game of Life. Dave Greene finally implemented my shield bug design, although changing one of the details resulted in the completed spaceship looking nothing like a shield bug whatsoever!
It’s an immense 934856 by 290486 pixels in size, making it (by area) much larger than the 17c/45 caterpillar that began the tradition of naming these large cumbersome track-laying spaceships after insects. The (23,5)c/79 and (13,1)c/31 projects appear to have been abandoned.
On an unrelated topic, a discussion with Tim Hutton and Simon Rawles in a pub in Cambridge has culminated in them investigating various embeddings of surfaces by crocheting them. Most recently Tim has produced a Chen-Gackstatter surface in this manner:

Another interesting blog by a computer scientist is that of Susan Stepney. One of her recent posts featured a video of a rendition of a particular music video in the Alexandroff Corridor of Newnham College, Cambridge, which Trinity has recently reproduced in an attempt to encourage the artist to perform at the forthcoming (149th) May Ball:
[youtube=http://www.youtube.com/watch?v=zfidVKFRVR0]
This has recently gained quite a lot of media attention across Europe, appearing in both a Spanish and a Croatian newspaper. Further bulletins as events warrant…


I think this new holyhedron is stretching the definition of a holyhedron a bit. At least according to wikipedia, the hole is not supposed to share points with the face boundary. Here it is even unclear if it is a single face or five coplanar ones.
There is even simpler “12-face” solution with the same property – a cube with a 3-dimensional “+” drilled through it.
Which face are you referring to? There are:
— 2 pentagons with pentagonal holes (definitely homeomorphic to the annulus)
— 10 trapezia with trapezial holes (again, definitely homeomorphic to the annulus)
In particular, this holyhedron is consistent with both Wikipedia and Conway’s original definition.
I don’t see a pentagonal face with a pentagonal hole in it. I see five coplanar trapezoid faces touching by corners. Even if I agree that they form a single face, the hole in the middle is still touching its circumference. Of course I can imagine the rest of the pentagon is hidden inside the volume of the polyhedron but I don’t think definition of a polyhedron face allows that. I don’t think parts of faces that are inside the volume of the polyhedron count – if that was the case, the 492-faced holyhedron would be invalid as we could imagine continuation of holes in its faces inside its volume. The whole 492-faced holyhedron was union of concave objects and “holes” in faces were only holes because something was “growing out” from the face.
Yes, the appearance of the annular pentagonal face is an optical illusion caused by the fact that this polyhedron is self-intersecting. As such, the notion of ‘inside the volume’ is meaningless; I haven’t even checked whether the polyhedron is orientable. Either way, it’s still a polyhedron according to the usual definition (Kepler-Poinsot solids are polyhedra).
Ah, okay, I think I got my head around it. So what is a polyhedron anyway? I found a bunch of different definitions and under some, a set of two faces stitched together by matching edges (a deflated/squished toroid) appears to be the minimum solution.
But I would kind of expect this to be “discovered” long ago if such kind of polyhedrons was considered valid initially.
@Kasuha A 24-faced self-intersecting holyhedron with the nice property of being isohedral was already discovered by Grünbaum and Shepard in 2003. I found out about this (through happening upon their paper) weeks after discovering the 13-facer. It probably went unnoticed because self-intersection is implicitly taboo…
@Nathan Ho: I assumed that the polyhedron for this challenge has to be a solid. I didn’t even know that a self-intersecting polyhedron is still called polyhedron. Without the “solidness” requirement, I think the minimum solution consists of two faces, six edges and six vertices – each face is a triangle with triangular hole in it, each edge joins two corresponding sides of the two faces. It sure matches a generic polyhedron definition but it feels too trivial to be considered valid solution of the challenge.
@Kasuha: You are right that there isn’t really a precise, universally accepted definition of polyhedron. However, all classifications of polyhedra I’ve seen (e.g. the Johnson solids, or Bonnie Stewart’s toroidal polyhedra) consider coplanar faces joined at an edge to be a degeneracy.
“Solidness” is not a very good restriction because, as apgoucher said, it excludes nonorientable polyhedra. The tetrahemihexahedron (which is nonorientable and self-intersecting) is pretty much universally considered a valid polyhedron.
Can the last shape (in the animated gif) be 3d-printed?