Proto-Penrose tilings

A while ago, Roger Penrose famously filed a lawsuit against Kimberly Clark when his wife discovered that a roll of quilted lavatory paper was adorned with his aperiodic tiling. Although the tiling occurs naturally in quasicrystals, Penrose was probably the first person to discover and abstractly formalise the pattern. Nevertheless, there have been several historical ‘near-misses’ which came close, and indeed would have yielded isomorphic tilings if applied recursively. Since we’ve already mentioned Penrose, it seems only natural to approach this in inverse chronological order.

Kepler’s monsters

It is unknown as to exactly why Johannes Kepler investigated this particular tiling, although one sensible suggestion is that he was trying to construct a tiling of the plane involving only shapes with D10 symmetry. For example, ten regular pentagons neatly fit around a regular decagon of the same edge length, and it is possible to continue the pattern further if pentacles are also allowed:

Unfortunately, however, it is not possible to continue this process forever. Pretty soon one is required to have decagons overlapping, as in this particular drawing by Kepler:

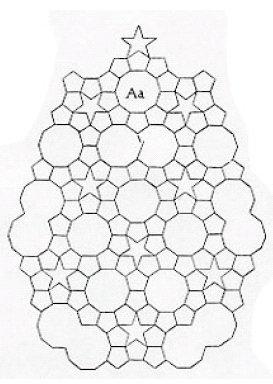
Kepler’s original drawing of the Kepler’s Monsters tiling.

With the assistance of these fused decagons, termed monsters by Kepler, it is possible to create various periodic and nonperiodic tilings of the plane. Craig Kaplan explored many variations on this theme in his article, with the Keplerian problem of finding a tiling using only (finitely many distinct) shapes of D10 symmetry remaining unsolved.

Even earlier were several attempts by Albrecht Dürer, whom you may know from his Melencolia I engraving inter alia. These featured pentagons and rhombi, similar to Penrose’s original tiling but with less sophisticated matching rules incapable of enforcing aperiodicity.

Girih tiles

I was in the Persian section of the Victoria and Albert Museum during the post-Christmas weekend at the end of last year, and happened to notice various geometric designs. Some of these were periodic carvings of knotwork, not unlike similar examples in the Alhambra in Moorish Spain.

Others were more exciting. One particularly ornate example features angles commensurate with the internal angles of a pentagon, and bears a striking similarity to the aforementioned tilings of Penrose, Kepler and Dürer:

Apparently these are formed from a set of five so-called Girih tiles, and patterns of a similar nature occurred throughout the Islamic world since the Middle Ages. In particular, I am intrigued to see the more sophisticated Girih tilings featuring patterns on two scales, where the small-scale pattern is created by applying a set of subdivision rules to the large-scale pattern. This is analogous to the method by which Penrose tilings can be constructed, as you will know from my online demonstration:

This surprising and fascinating connection between Islamic architecture and quasicrystalline tilings was first discovered and investigated by Paul Steinhardt and Peter Lu, the latter of whom presented an exposition on the subject at the Harvard Physics Colloquium:

If you found this interesting, there is a talk on early Islamic mathematics by Dr. Bursill-Hall at 16:00 today in Meeting Room 3 of the Centre of Mathematical Sciences.

Miscellany

Finally, I have a few late items of news. Stuart Gascoigne has just sent in the first 8192 2-adic valuations of polylogarithms. The ‘spike’ in the last row (associated with 8192) penetrates significantly deeper into the grid, with Q(3, 8181) being the first integer of the form 64n + 53:

Here are some other recent highlights:

• Eugenia Cheng has committed a third instance of gastro-mathematical marketing, namely a formula for the perfect doughnut.
• Alex Bellos and I attended a pre-release viewing of X+Y, an action thriller following the romantic life of a British olympiad contestant. Expect a review from us next month.
• Jeffrey Ventrella has been investigating self-similar fractal curves for a while, and recently sent me this analysis of fractal curves based on Gaussian and Eisenstein integers.