Amidst Saturday’s turmoil, the following problem came into consideration:
There are plans to build a nuclear power station on an initially empty 12-by-12 chessboard. Doing so would require an empty 4-by-3 or 3-by-4 rectangular region of squares. To foil this plan, Jeremy decides to erect coal mines on squares of the chessboard (with each mine occupying a single square) to ensure there is no sufficiently large empty rectangle. What is the minimum number of coal mines necessary for Jeremy to prevent the construction of the nuclear power station?
With little effort, one can obtain a lower bound of 12 by partitioning the chessboard into twelve disjoint rectangles, noting that each one must contain at least one mine:
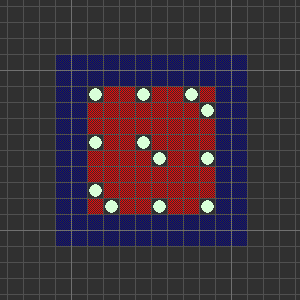
Similarly, we can establish an upper bound of 16 by placing a mine at (x, y) if and only if x and y are both divisible by 3. Can this bound be improved? In particular, note that it is never wise to place a coal mine near the edge of the board, since we can move it inwards without reducing its effectiveness for blocking potential nuclear power plants. Without loss of generality, we will therefore only consider arrangements where the mines are in the 8-by-8 ‘reasonable region’ in the middle of the board:
One reasonable approach is to place mines on the boundary of this region, and then concentrate on the centre of the board. This reduces the upper bound from 16 to 12, and is therefore optimal:
What about a larger board? In particular, what is the lowest density of mines that can be placed on the infinite plane to leave no 4-by-3 or 3-by-4 rectangle unoccupied? Again we have a lower bound of 1/12 and an upper bound of 1/9. The upper bound can actually be reduced to 1/10 by using the following lattice:
It appears that it would be difficult, if not impossible, to improve upon this. Observe that if an empty 3-by-3 box occurs in any valid configuration, then there must be a coal mine in each of the four surrounding 1-by-3 boxes. Moreover, the lattice shown above achieves this bound, and has no 3-by-3 boxes containing more than one mine.
But how would one prove optimality? Given an arrangement of mines, we define a scoring function over by means of a convolution. Specifically, each mine contributes a score to its own square and those surrounding it as follows:
That is to say, each mine contributes a score of 20 to its own cell, 15 to the four edge-adjacent cells, 16 to the four other vertex-adjacent cells, 4 to the four cells at a distance of 2 in a horizontal or vertical direction, and 5 to each of the eight cells a knight’s move away from the mine.
Then the score associated with a given square is simply the sum of the contributions from nearby mines.
This may appear to be a seemingly arbitrary scoring function, but it was chosen to exhibit the following properties:
- The score associated with the density-1/10 lattice is uniform across all cells (and equal to 20);
- For any valid configuration (one with no 3-by-4 or 4-by-3 empty rectangle), every cell gets a reasonably high score (in this case, the minimum possible is 15).
Since the total score contributed by each mine is 200, we can determine the density by dividing the average score by 200. Hence, proving that the density-1/10 lattice is optimal is equivalent to the following statement:
The average score in any valid configuration must be at least 20.
It transpires that this is true, and can be obtained by locally perturbing the scoring function (without violating conservation of total score) so that no cell has a score below 20. This is a finite check, and sufficiently small that it can be performed without the assistance of a computer.
Suppose we have a cell with a score strictly less than 20. It is easy enough to show that one of the following two possibilities must arise:
- Case I: The score is 19, and the cell is positioned between two mines like so:
- Case II: The cell belongs to precisely one empty 3-by-3 region, which is surrounded by four mines.
We deal with all instances of Case I before Case II, by incrementing each ’19’ and decrementing the two cells which are edge-adjacent to the ’19’ and vertex-adjacent to the neighbouring mine. This actually decreases the overall score, so (if we can show that the average score is still at least 20) any configuration with an example of Case I is suboptimal.
Case II is more complicated to address than Case I, because each of the four mines surrounding the 3-by-3 region can be in any of three possible positions. Moreover, empty 3-by-3 regions can potentially overlap slightly. Nevertheless, if we consider only the portion of the 3-by-3 region which belongs to no other 3-by-3 regions, the average score is still at least 20, with equality if and only if the mines are arranged to resemble a portion of the density-1/10 lattice. This is true even after we perform any reductions associated with Case I.
Convincing yourself is a matter of testing each of the possible sub-cases for Case II (there are at most 81, and this quickly reduces when you take symmetry into account).
What have convolutions ever done for us?
In addition to solving this rather niche problem in Corbynatorial geometry, convolutions have a wealth of other applications.
- Even if we restrict ourselves to considering convolutions of an arbitrary function on a square grid with a small finitely-supported kernel, this is useful for image-processing. Common edge-detection algorithms use this concept, right up to the sophisticated convolutional neural networks underlying Google’s image recognition software. These are explained very clearly in various places.
- A continuous analogue is taking a convolution of measurable functions over
or the torus obtained by quotienting by a lattice. Gaussian kernels are often used.
- More generally, one can convolve continuous functions over an arbitrary compact group. In the cases where the group is Abelian, this can be computed quickly by means of a Fourier transform (although this is typically overkill when the kernel has small finite support).






Hey, that was a long break!
There is a mistake below the first picture: “lower bound” should actually be “upper bound”.
Well spotted.