Subsumptions of regular polytopes

We say that a regular n-dimensional polytope P subsumes a regular n-dimensional polytope Q if the vertex-set of Q is geometrically similar to a subset of the vertex-set of P.

For instance, the dodecahedron subsumes a cube (the convex hull of the red and blue vertices below), which in turn subsumes a tetrahedron (the convex hull of the blue vertices alone):

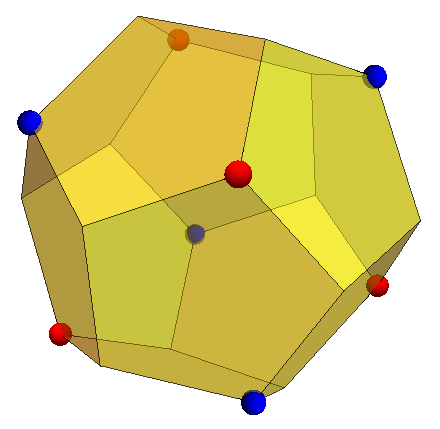
Note that the centroid of a regular polytope is also the circumcentre — the unique point equidistant from all of the polytope’s vertices — which implies that if one polytope subsumes another, the two vertex-sets must share the same centre. Consequently, we assume without loss of generality that regular polytopes are always centred on the origin.

Two and three dimensions

The only regular polytopes in two dimensions are the regular polygons. Using the above reasoning, it is straightforward to see that an m-gon subsumes an n-gon if and only if n is a divisor of m.

In three dimensions, there are exactly five regular polytopes, the Platonic solids. We have already seen that the tetrahedron, cube, and dodecahedron form a chain of subsumptions. It can be shown that these are the only subsumptions between Platonic solids. In particular, if we normalise the solid P to be centred on the origin and have unit radius, we can calculate the set S(P) of pairwise inner products between the vertices of the polyhedron. If P subsumes Q, then S(Q) must necessarily be a subset of S(P).

Four dimensions

In four dimensions, there are six ‘Platonic solids’. Five of these form a subsumption chain:

• the orthoplex (generalised octahedron) is subsumed by
• the hypercube, which is subsumed by
• the 24-cell, which is subsumed by
• the 600-cell, which is subsumed by
• the 120-cell.

There’s a really elegant way to see these inclusions in terms of quaternions. The group Q8 of eight quaternions {±1, ±i, ±j, ±k} form the vertices of an orthoplex.

This is an index-3 subgroup of the binary tetrahedral group, which contains these eight quaternions together with the 16 unit quaternions of the form:

½(±1 ± i ± j ± k)

These 16 quaternions manifestly form the vertices of a hypercube. Moreover, because we can partition the binary tetrahedral group into cosets with respect to the subgroup Q8, it follows that this hypercube is the union of two disjoint orthoplexes. Taken together, these 24 quaternions form the vertices of a 24-cell, a four-dimensional regular polytope which has no analogue in three dimensions.

Greg Egan’s animation below shows the three cosets in red, green, and blue. Each coset forms the vertices of an orthoplex; the union of any two cosets forms the vertices of a hypercube; the union of all three cosets forms the vertices of a 24-cell:

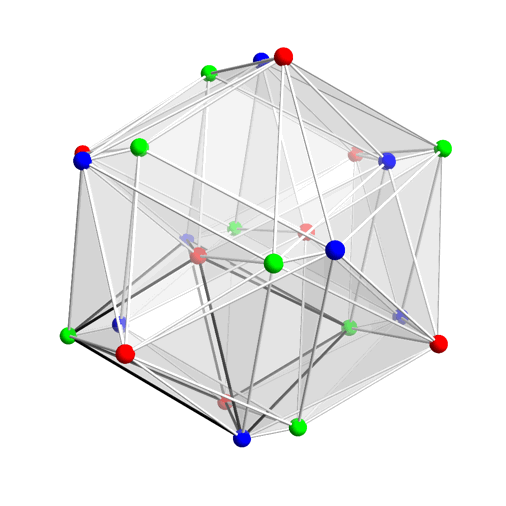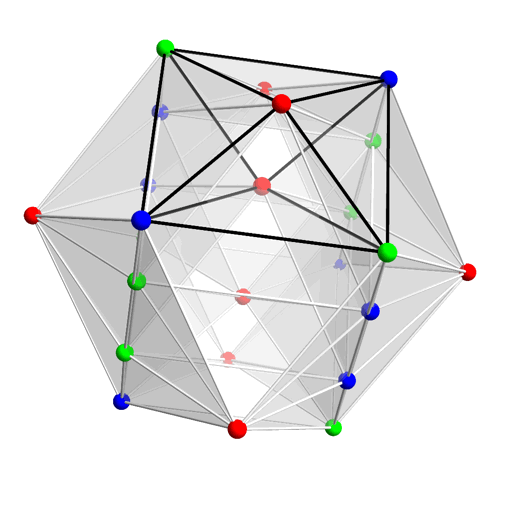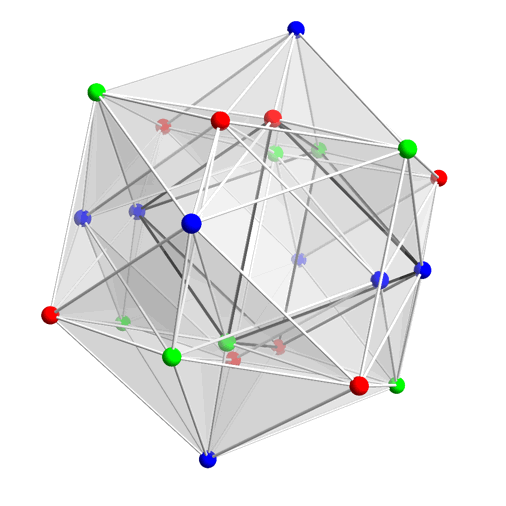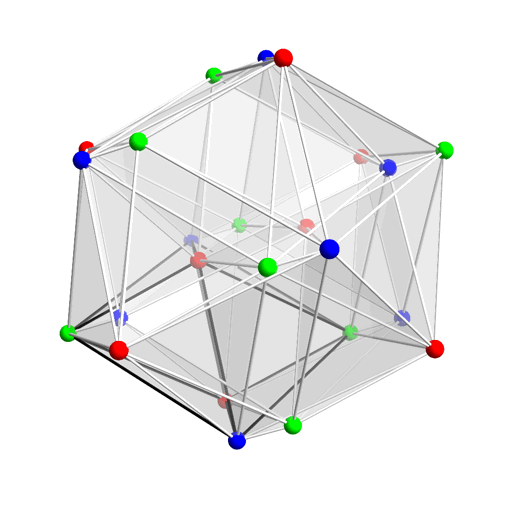
Animation by Greg Egan of a 24-cell undergoing a double rotation.

The 600-cell has 120 vertices which can be identified with the unit icosians, a group of 120 unit quaternions which contains the binary tetrahedral group as an index-5 subgroup. It follows, therefore, that the 600-cell subsumes the 24-cell.

If you take the ring generated by the unit icosians, the 600 norm-2 elements form a scaled copy of the 120-cell, a four-dimensional analogue of a dodecahedron. We can identify norm-2 elements if one can be obtained from the other by right-multiplication by a unit icosian; this partitions these 600 vertices into five equivalence classes, each geometrically similar to the 120 vertices of a 600-cell.

The remaining four-dimensional regular polytope, the simplex, is subsumed only by the (600-vertex) 120-cell. [EDIT: This was amended from the previous (incorrect) statement that the simplex is not subsumed by any of the other polytopes.]

Higher dimensions

In higher dimensions, there are only three regular polytopes: the simplex, the orthoplex, and the hypercube.

S(simplex) is the set {1, −1/n}, and S(orthoplex) is the set {1, 0, −1}. It follows that neither of these can subsume each other. This leaves the question of whether the hypercube can subsume either of the other two regular polytopes. The answer is that it depends on n, and is an unsolved problem!

The orthoplex consists of n orthogonal pairs of opposite vertices. For this to be subsumed by a hypercube is equivalent to the existence of a matrix M consisting entirely of entries ±1 such that H := M / √d is a real orthogonal matrix. Such Hadamard matrices exist whenever n is a power of 2. If n ≥ 3, it is easy to show that n must be a multiple of 4, and the converse is conjectured to be true:

Does a Hadamard matrix exist in dimension n whenever n is divisible by 4?

The first unsolved case is n = 668.

When does the hypercube subsume a simplex? This is equivalent to having n+1 vectors with entries ±1 such that, for every pair of vectors, they disagree in sign in (n+1)/2 coordinates and agree in sign in the other (n−1)/2 coordinates. If we appended an (n+1)th coordinate which is identically 1 to every vector, they would all be orthogonal and therefore form a Hadamard matrix. The converse is also true: removing a column of a Hadamard matrix results in a set of rows which form the vertices of a regular simplex.

To conclude:

• The hypercube subsumes the simplex if and only if there is a Hadamard matrix of dimension n+1;
• The hypercube subsumes the orthoplex if and only if there is a Hadamard matrix of dimension n.