For any nonnegative integer n, there exists the highly symmetric Barnes-Wall lattice in dimension . In low dimensions, these are (up to scaling and rotation) familiar lattices:
- For n = 0, this is just the integer lattice,
.
- For n = 1, the lattice is
, a scaled and rotated copy of the familiar square lattice
.
- For n = 2, we obtain the
lattice (consisting of all integer points with even coordinate sum). The convex hull of the vectors closest to the origin form a 24-cell, a self-dual regular polytope in four dimensions.
- For n = 3, this is a scaled copy of the
lattice, discovered by Thorold Gosset and proved by Maryna Viazovska to be the densest packing of unit spheres in eight-dimensional space.
- For n = 4, this is a scaled copy of the 16-dimensional laminated lattice,
, which again is the densest known lattice packing in its dimension. In Conway and Sloane’s Sphere Packings, Lattices and Groups, this is additionally described as a section of the Leech lattice.
We’ll describe a construction of the Barnes-Wall lattices that makes their full symmetry groups apparent (with the unavoidable exception of n = 3). Unlike the other simple constructions of the Barnes-Wall lattices, which involve quadratic fields, this construction only makes use of the classical integers .
The real Clifford group and the minimal vectors
Being slightly notationally liberal (denoting a Weyl group by the name of its Dynkin diagram), let be the symmetry group of a standard 24-cell. It has order 1152. In particular, it contains an index-3 subgroup consisting of the 384 signed permutation matrices; the remaining 768 elements are precisely the 4-by-4 Hadamard matrices (see previous post), appropriately scaled so as to be orthogonal matrices.
Being extremely notationally liberal, for n ≥ 3 we let be generated by:
- the symmetric group
, which acts naturally on
when considered as an n-fold tensor product of
with itself;
- the group
, where we expand each of the
matrices to a
matrix by taking the Kronecker product with a
identity matrix.
Equivalently, in the language of minimalistic quantum computation, it’s the group generated by (real orthogonal) 2-qubit gates with dyadic rational entries. (These are exactly elements of F_4 conjugated by elements of S_n.)
Technically, we’ve only defined the groups for n ≥ 2. For completeness, we define F_1 and F_2 to be the groups of signed permutation matrices in dimensions 1 and 2, respectively. To cover these cases, we can amend the previous definition to:
For any nonnegative integer n,
is the group of n-qubit gates generated by the dyadic rational gates acting on at most 2 qubits.
Then the minimal vectors of the Barnes-Wall lattice in dimension are just the images of the all-ones vector (1, 1, …, 1) under the action of this real Clifford group
. The number of such vectors is given by A006088, and the Euclidean length of each vector is
.
We can then simply define the Barnes-Wall lattice to be the lattice generated by these minimal vectors! The determinant of the lattice is .
The full symmetry group
Whenever n ≠ 3, the symmetry group of the lattice is exactly the real Clifford group described above, with order given in A014115.
When n = 3, however, the symmetry group of the lattice is 270 times larger! Rather than just being , it additionally contains arbitrary permutations of the eight coordinates, and is the Weyl group of
.
A generator matrix
It is convenient to have an integral basis of this lattice, compatible with the described construction. In particular, the basis vectors will be a convenient subset of the minimal vectors, and moreover will lie on the vertices of the cube .
Greg Kuperberg describes an elegant construction of an integral basis of minimal vectors in a scaled and rotated copy of the Barnes-Wall lattice. In particular, he takes the (n-1)-fold tensor product of the matrix [[1, 1], [1, i]] and then replaces each of the resulting (complex) entries a + bi with a 2-by-2 real matrix [[a, b], [-b, a]].
We’ll modify this construction slightly by multiplying the (n-1)-fold tensor product by the scalar 1 + i. This corresponds to scaling and rotating the lattice such that it agrees with our construction, and has the elegant property that every entry of the resulting real matrix is ±1. We’ll also permute the rows so that the matrix is symmetric.
The first six generator matrices are shown below:
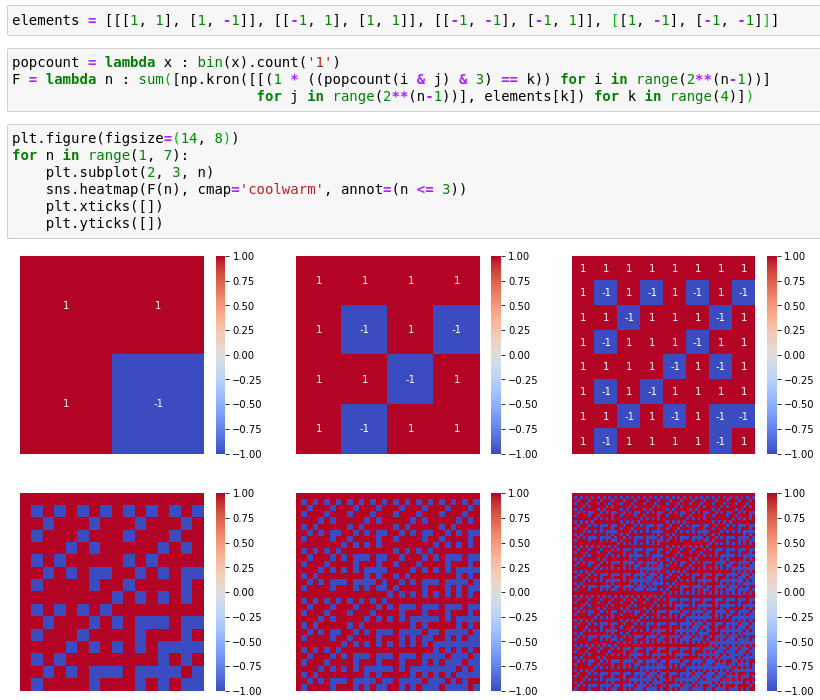
The code above uses the following equivalent formulation:
- Take an M-by-M array, where
, and number the rows/columns in a 0-indexed fashion.
- Define the weight of the (i, j)th entry to be popcount(i & j). That is to say, we take the size of the intersection between the set of ‘1’-bits in the binary expansions of i and j.
- Populate the (i, j)th entry with a 2-by-2 symmetric matrix according to the weight modulo 4:
- if 0 modulo 4, use the matrix [[1, 1], [1, -1]];
- if 1 modulo 4, use the matrix [[-1, 1], [1, 1]];
- if 2 modulo 4, use the matrix [[-1, -1], [-1, 1]];
- if 3 modulo 4, use the matrix [[1, -1], [-1, -1]].
(These are precisely the four real symmetric 2-by-2 (±1)-matrices which square to 2I.)
Related reading
Other constructions of the Barnes-Wall lattices appear in:
- Gabriele Nebe, E. M. Rains, and Neil Sloane, A Simple Construction for the Barnes-Wall Lattices (using the ring
).
- Daniele Micciancio and Antonio Nicolosi, Efficient Bounded Distance Decoders for Barnes-Wall Lattices (using the ring
of Gaussian integers).
- Conway and Sloane, Sphere Packings, Lattices and Groups (using Reed-Muller codes).

When I was young and naïve, I conjectured there was nothing special about the Euclidean metric. Why should the Lp exponent be 2, why shouldn’t it be arbitrary? Then I learned that 2 minimized the value of pi, which curved back toward 4 as you moved toward one or infinity. The more I learn the more naturally special 2, 3, and 4 dimensional spaces feel, and here yet again is a nugget of evidence that something happens in 3D that is absent elsewhere!
Very tangentially related, but letting the Lp metric exponent vary turned out to be a convenient way to animate a gameplay feature! (http://entropygames.net/files/shared/deformers/blockmath.gif) But there are probably lots of good ways to blend between spheres and cubes 🙂