Recall that the logarithm function (defined on the punctured complex plane) is multi-valued, with the different solutions to exp(x) = y differing by integer multiples of 2πi.
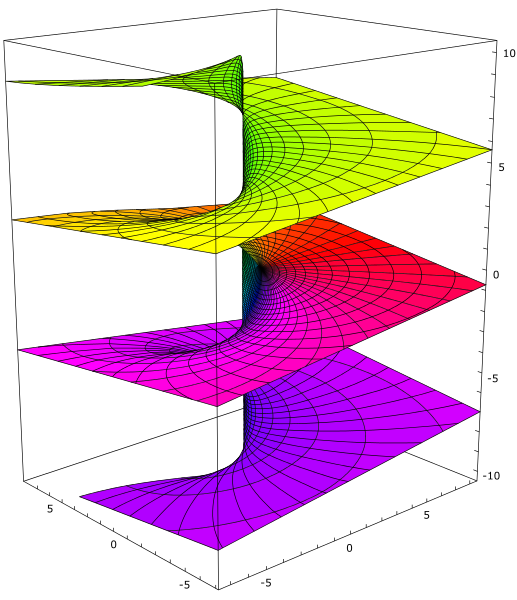
Visualisation of the imaginary part of the multi-valued complex logarithm function, created by Leonid 2.
James Propp remarked that the values of the form i^i^i are a dense subset of the unit circle. Extending this, one can show that the values of the form i^i^i^i are not dense in the complex plane, but those of the form i^i^i^i^i are.
Defining the EL-numbers
Timothy Chow described an interesting subfield of the complex numbers, known as either closed-form numbers or (less ambiguously) EL-numbers. We’ll present a slightly different but equivalent definition here, where we embrace the complex logarithm function in its full multivalued glory instead of choosing a principal value of the logarithm function.
In particular, the EL-numbers can be defined as follows:
- Zero: the complex number 0 is an EL-number;
- Addition/subtraction*: given two EL-numbers, a and b, then f(a, b) is also an EL-number where c = f(a, b) is the solution to a + b + c = 0;
- Exponentiation: given an EL-number x, then exp(x) is also an EL-number;
- Logarithm: given a nonzero EL-number y, then (at least**) one solution of exp(x) = y is also an EL-number.
*this slightly unconventional operation f, which is equivalent to having both addition and subtraction rules, was chosen because it’s completely symmetric: the validity of c = f(a, b) is invariant under permutation of a, b, and c. The relevance of this will become apparent in a future post.
**we show that this implies that all solutions are EL-numbers, so this definition is well-defined.
The first two rules provide us with unary negation and addition, so we know that the EL-numbers form an additive group:
- −x = f(x, 0);
- x + y = f(f(x, y), 0).
Togther with the other two rules, we can show that the EL-numbers form a field. In particular, if x and y are nonzero, then exp(log(x) + log(y)) = xy and exp(−log(x)) = 1/x irrespective of which choices of logarithms were taken. Finally, we need the multiplicative identity 1 to exist, but that can be obtained straightforwardly as exp(0).
Consequently, every rational number is a deterministic EL-number: we can, for each rational q, write down an expression which evaluates to q irrespective of which choices of logarithms are taken. Other deterministic EL-numbers include e, which can be obtained as exp(exp(0)). More generally, every element of the smallest field containing the rationals and closed under exponentiation is also a deterministic EL-number, and we conjecture that the converse is also true.
Mitigating multivaluedness
To show that we can obtain all logarithms (not just one), we apply the following procedure:
- Apply the logarithm rule to obtain some solution x to exp(x) = y. This may be different from the ‘desired’ solution, w;
- Apply the logarithm rule to obtain some solution p to exp(p) = −1. This is necessarily some odd integer multiple of πi.
- We know that w − x is therefore a rational multiple of p, say qp, so we can construct q deterministically, multiply it by p, and add the result to x to obtain w.
Note that this was somewhat ‘interactive’: we needed to know what solutions x and p were obtained in order to choose the correct rational number q to use. The ‘closed-form expression’ for w depends on the branches of the logarithms taken, and each of these expressions are ‘nondeterministic’ in the sense that if someone changed which branches were taken, they would no longer define w.
Nondeterministic EL-numbers
Clearly, some deterministic EL-numbers can have nondeterministic expressions: for example, exp(log(exp(0))/2) can be either 1 or −1, even though these are both deterministic EL-numbers. Are there any EL-numbers which only have nondeterministic expressions?
Well, yes: the imaginary unit i can be obtained as exp(log(−1) / 2). We’ll call this a nondeterministic EL-number, because any closed-form expression for i is also a closed-form expression for −i. By the same argument (namely the fact that complex conjugation is an exponential field automorphism of the complex numbers), every nonreal EL-number is necessarily nondeterministic.
π is also an EL-number, because both πi and i have already been shown to be EL-numbers, and we know that they form a field. Is it a deterministic EL-number? Certainly it hasn’t been proved that this is not the case, because it hasn’t even been shown that e + π is irrational. But on the other hand, it seems very difficult to find a construction of π that doesn’t also end up constructing an infinite number of other multiples of π.
My suspicion is that π is not a deterministic EL-number — can this be proved, conditional on a plausible assumption such as Schanuel’s conjecture?

Maybe it is reasonable to consider logarithm of zero an EL-number as well. https://mathoverflow.net/q/432396/10059