In the early 1930s, Pascual Jordan attempted to formalise the algebraic properties of Hermitian matrices. In particular:
- Hermitian matrices form a real vector space: we can add and subtract Hermitian matrices, and multiply them by real scalars. That is to say, if
and
are Hermitian matrices, then so is the linear combination
.
- We cannot multiply Hermitian matrices and obtain a Hermitian result, unless the matrices commute. So the matrix product
is not necessarily Hermitian, but the ‘symmetrised’ product
is Hermitian, and coincides with ordinary multiplication whenever the matrices commute.
Now, this symmetrised product is commutative by definition, and is also (bi)linear:
. What other algebraic properties must this product satisfy? The important ones are:
- Power-associativity: the expression
does not depend on the parenthesisation.
- Formal reality: a sum of squares is zero if and only if all of the summands are zero.
The second of these conditions means that we can say that an element of the Jordan algebra is ‘nonnegative’ if it can be expressed as a sum of squares. (In the familiar context of real symmetric matrices, this coincides with the property of the matrix being positive-semidefinite.) The nonnegative elements form a ‘cone’ closed under multiplication by positive real scalars and addition.
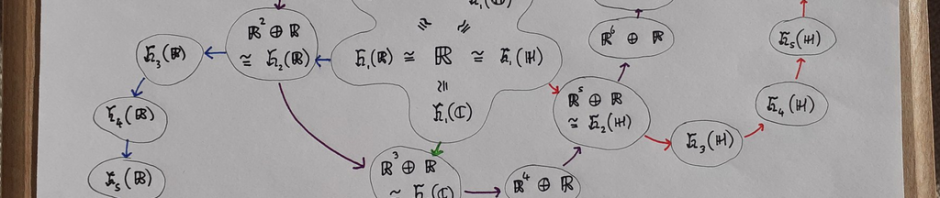
Jordan, von Neumann, and Wigner proceeded to classify all of the finite-dimensional algebras of this form (known as formally real Jordan algebras). They showed that every such algebra is a direct sum of ‘simple’ algebras, each of which is isomorphic to [at least] one of the following:
- the real symmetric matrices of dimension n (for any positive integer n) with the aforementioned symmetrised product;
- the complex Hermitian matrices of dimension n;
- the quaternionic Hermitian matrices of dimension n;
- the octonionic Hermitian matrices of dimension n (where n ≤ 3);
- the algebras
with the product
, known as ‘spin factors’. As John Baez mentions, these can be identified with Minkowski space, and the nonnegative elements are exactly the ‘future cone’ of the origin.
The qualification ‘at least’ is because there are some isomorphisms here:

Simple formally real Jordan algebras, showing the four infinite families and the exceptional Jordan algebra
Exactly one of these simple formally real Jordan algebras fails to fit into any of the four infinite families. This exceptional Jordan algebra is , the 3-by-3 self-adjoint octonionic matrices endowed with the symmetrised product. Viewed as a real vector space, it is 27-dimensional: an arbitrary element can be described uniquely by specifying the three diagonal elements (which must be real) and three lower off-diagonal elements (which can be arbitrary octonions); the three upper off-diagonal elements are then determined.
Projective spaces from Jordan algebras
Given a formally real Jordan algebra, we can consider the idempotent elements satisfying . For the Jordan algebras built from n-by-n real, complex, or quaternionic matrices, these are the matrices with eigenvalues 0 and 1.
We get a partial order on these ‘projection’ matrices: A ‘contains’ B if and only if . This partially-ordered set can be identified with the stratified collection of subspaces in the (n−1)-dimensional projective space over the base field:
- the zero matrix corresponds to the empty space;
- the rank-1 projection matrices correspond to points;
- the rank-2 projection matrices correspond to lines;
- …
- the rank-(n−1) projection matrices correspond to hyperplanes;
- the identity matrix corresponds to the full projective space itself.
The exceptional Jordan algebra gives us the octonionic projective plane, discovered by Ruth Moufang. We can’t get any higher-dimensional octonionic projective spaces because Desargues’ theorem is false in the octonionic projective plane, whereas it’s true in any plane that can be embedded in a 3-dimensional projective space. We mentioned this seven years ago.
This hints at why 4-by-4 and higher octonionic matrices have no hope of forming a formally real Jordan algebra: we’d be able to define an octonionic projective 3-space, which is impossible.
What about the spin factors? The idempotents in are:
- the zero element (0, 0), corresponding to the ’empty space’;
- the identity element (0, 1), corresponding to the ‘full space’;
- the points (x, ½) where x is an arbitrary vector of length ½.
In other words, these correspond to spheres! Recall that the real, complex, quaternionic, and octonionic projective lines are (as topological manifolds) just the 1-, 2-, 4-, and 8-spheres, respectively; we can think of the spin factors as ‘projective lines’ built from arbitrary-dimensional spheres.
As for non-simple formally real Jordan algebras, the corresponding ‘projective spaces’ are just Cartesian products of the ‘projective spaces’ corresponding to the direct summands.
An exotic spacetime
In August of this year, Blake Stacey posted the following comment on John Baez’s essay:

Now for some context: it is possible to define the determinant of a 3-by-3 octonionic Hermitian matrix, and the group of linear operators (viewing as a 27-dimensional real vector space) that preserves the determinant is a noncompact real form of the Lie group E6.
This group E6 is transitive on the positive-definite matrices of determinant 1. The subgroup fixing any one of these (without loss of generality, the identity matrix) is the compact real Lie group F4, which also preserves the Jordan product. This means that it maps idempotents to idempotents, so can be seen as acting on the octonionic projective plane as its group of projective transformations.
This group F4 is transitive on the rank-1 idempotent matrices, and the subgroup fixing any one of these is Spin(9). (As a result, we can describe the octonionic projective plane as the quotient F4 / Spin(9). Elie Cartan proved that all compact Riemannian symmetric spaces are quotients of compact Lie groups.)
What’s the analogy for familiar (3+1)-dimensional Minkowski spacetime?
- the full group (analogous to E6) is the proper orthochronous Lorentz group;
- the subgroup fixing a timelike vector (analogous to F4) is the rotation group SO(3);
- the subgroup additionally fixing a lightlike vector (analogous to Spin(9)) is the rotation group SO(2);
- the symmetric space (analogous to the octonionic projective plane) is the quotient SO(3) / SO(2), which is just the familiar 2-sphere.
A lattice in this exotic spacetime
It is natural to consider the ‘integer points’ in this spacetime, namely the octonionic Hermitian matrices where the off-diagonal elements are Cayley integers and the diagonal elements are ordinary integers. John Baez mentions that this is the unique integral unimodular lattice in (26+1)-dimensional spacetime, and it can be seen as the direct sum of the exceptional Lorentzian lattice with a copy of the integers.
This lattice was thoroughly investigated in a marvellous paper by Noam Elkies and Benedict Gross. Possibly the most surprising discovery in this paper is that whilst E6 acts transitively on the positive-definite matrices of determinant 1, this no longer holds when you ‘discretise’! More precisely, the positive-definite ‘integer points’ of determinant 1 form two distinct orbits under the discrete subgroup of E6 that preserves the lattice.
One of these orbits contains the identity matrix; the other contains the circulant matrix with elements {2, η, η*} where . [Note: there’s a 6-dimensional sphere of octonionic square-roots of -7. You’ll need to choose one that results in η being a Cayley integer.] If you use this other matrix E as your quadratic form instead of the identity matrix I, this leads to a very natural construction of the Leech lattice.
Specifically, as shown in the Elkies-Gross paper, triples of Cayley integers with the norm form an isometric copy of the Leech lattice! By contrast, the usual inner product
using the identity matrix as the quadratic form gives the direct sum
— again an even unimodular lattice in 24 dimensions, but not as exceptional or beautiful or efficient as the Leech lattice.
Further reading
To get a full understanding of the octonions, Cayley integers, and exceptional Jordan algebra, I recommend reading all of the following:
- John Baez’s articles on integral octonions;
- On Quaternions and Octonions, by Conway and Smith;
- The Exceptional Cone and the Leech Lattice, by Elkies and Gross.
Robert Wilson has also constructed the Leech lattice from the integral octonions (see here and here). Wilson’s construction also involves , so it may be possible to show reasonably directly that it’s equivalent to the Elkies-Gross construction.