Breaking news: Patrick Stevens (whom you may recognise from the cp4space cipher-solving leaderboard) has published a collection of poems pertaining to Sylow’s theorems.
Anyway, on the real projective plane, there are a couple of geometric theorems worth mentioning. The thing that’s interesting about Pappus’ theorem and Desargues’ theorem is not that they apply to the real projective plane, but rather that whether or not these theorems apply to a particular projective plane can be used to deduce properties of how the plane was constructed. I’ll start by stating the theorems:
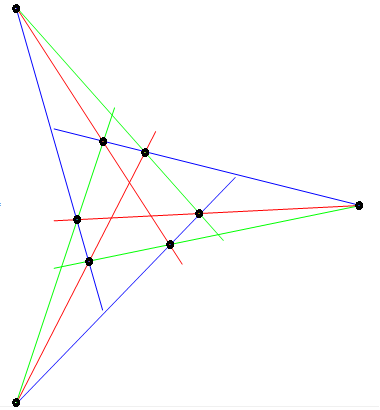
Pappus’ theorem: If we have eight of the nine concurrences shown in the diagram above, then the ninth also holds. In the complex projective plane, this follows from the Cayley-Bacharach theorem.
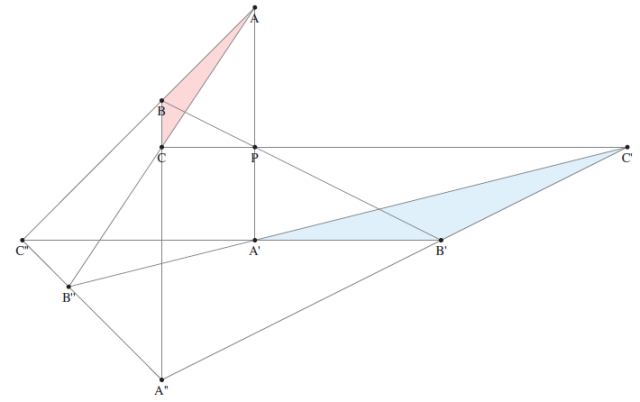
Desargues’ theorem: Two triangles are in perspective about a point if and only if they are in perspective about a line (see above). Equivalently, suppose we have a collection of 10 points and 10 lines, associating an ordered pair (p(V), l(V)) of a point and a line to each vertex V of the Petersen graph, where each edge is replaced with a zweibeck (pair of oppositely directed edges). We consider each directed edge X → Y to represent the point p(X) and the line l(Y). Desargues’ theorem states that if 29 of these correspond to incidences (a point lying on a line), then so does the thirtieth.
A German mathematician called Hessenberg proved that Desargues’ theorem can actually be deduced from Pappus’ theorem. In other words, all Pappian projective planes are also Desarguesian. For example, the real and complex projective planes, and the projective planes of finite order, are all Pappian, so thus Desarguesian.
The converse of Hessenberg’s theorem is not true, however. The quaternionic projective plane is Desarguesian, but not Pappian. It transpires that this is a consequence of the quaternions being non-commutative. Indeed, the following have been proved:
- Every Desarguesian plane can be constructed from a skew-field F, by working in the vector space F³, discarding the origin and identifying scalar multiples of a point. The converse is also true.
- The Pappian planes are precisely those constructed from a commutative field F.
This is quite remarkable, since non-Desarguesian planes can be really bizarre. Some correspond to this sort of construction (e.g. the octonionic projective plane, or Cayley plane), whereas others are downright pathological (e.g. the Moulton plane).
If a plane can be embedded in a three-dimensional projective space, it is automatically Desarguesian. Consequently, it is impossible tohave an octonionic 3-space , as that would imply that the Cayley plane is Desarguesian (which it isn’t). The proof of this is quite simple, and follows from letting ABC and A’B’C’ in the diagram be triangles in different planes (so A”B”C” must trivially be the line where the planes intersect), and projecting down into two dimensions.

Pingback: Ten things you (possibly) didn’t know about the Petersen graph | Complex Projective 4-Space
Pingback: Desert Island Theorems | Complex Projective 4-Space
A
Pingback: The exceptional Jordan algebra | Complex Projective 4-Space