In January 2000, Erich Friedman considered the problem of finding a rigid unit-distance graph G containing a regular heptagon as a subgraph. That is to say, the graph is immersed in the plane such that:
- every edge of G must have unit length;
- there exists some ε > 0 such that any ε-perturbation of the vertices of G results in at least one of those edges having non-unit length;
- G contains a subgraph H isomorphic to a 7-cycle, such that the vertices and edges of H are those of a regular heptagon.
Last year, Watanabe Masaki discovered a solution where G has only 59 edges:
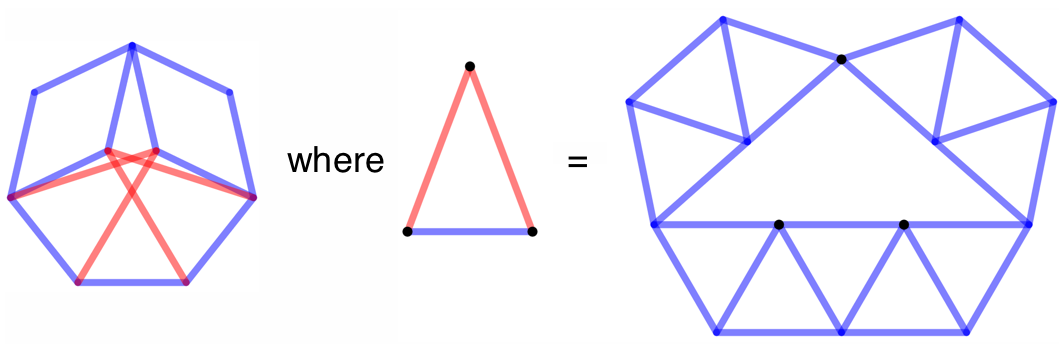
Watanabe Masaki’s 59-edge solution (blue lines represent edges)
On 19th December, Ed Pegg asked on Math StackExchange whether the following 42-edge configuration (invariant under an order-7 cyclic group of rotations, same as the heptagon) is rigid:
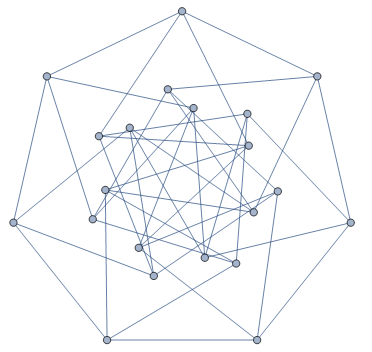
Ed Pegg’s 42-edge candidate graph
Jeremy Tan and William R. Somsky independently and concurrently proved that Pegg’s graph is indeed rigid, and that some of the vertices are redundant: it can be reduced to a 35-edge subgraph with the same rigidity property, significantly improving on Masaki’s upper bound of 59:
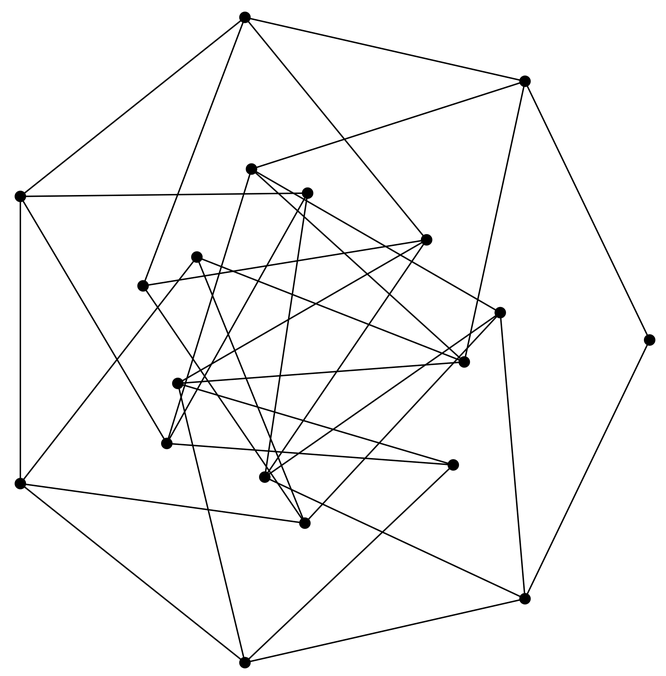
Jeremy’s 35-edge subgraph
Tan won the race by a narrow margin, posting a proof whilst Somsky was still writing up his solution. The proof also mentions that this graph is minimal (no proper subgraph is a solution), but it is an open problem whether the graph is minimum (has the smallest number of edges amongst all solutions).
This raises the question: can you find a solution with 34 or fewer edges?
In the other direction, what lower bounds can you find? A minimal example must be a Laman graph and therefore have 2n − 3 edges where n is the number of vertices. Each additional vertex can only be adjacent to at most 2 of the original vertices (by unit-distance-ness), so we have:
2n − 3 = (number of edges) <= ((n − 7) choose 2) + 2(n − 7) + 7
which gives a lower bound of 4 new vertices (11 vertices total) and 19 edges. The gap between my rather weak lower bound of 19 and Jeremy Tan’s upper bound of 35 is vast; can we narrow it in either direction?
Other news
Siobhan Roberts has published an article in the New York Times for the 50th anniversary of Martin Gardner’s initial publication of Conway’s Game of Life. The article mentions several recent discoveries, including the period-21 spaceship discovered by John Winston Garth using the search program ikpx2 described in a previous post.
Around the same time the article was published (and therefore too late to be mentioned therein), Dylan Chen discovered a 3c/7 spaceship he named ‘Anura’. It is the second elementary 3c/7 spaceship to be discovered (after Tim Coe’s spaghetti monster) and by far the smallest (313 cells, as opposed to 702 for the spaghetti monster).
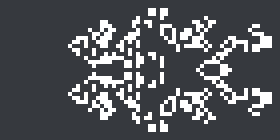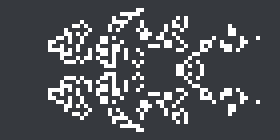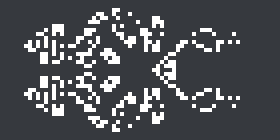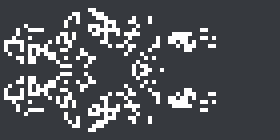
Dylan Chen’s new 3c/7 spaceship, Anura.
