Yes, the title sounds very counterintuitive. After all, don’t digital signature schemes require the general public to know your public key so that they can verify your signatures?
That is correct, but importantly they don’t need to know your public key until the very moment that you actually want to sign something. Instead, you can publish a hash of your public key long beforehand, and only publish your public key at the moment you digitally sign the message. The verifier then checks that the digital signature is valid using that public key, and then also checks that the public key is consistent with the hash you published.
The pseudonymous inventor of Bitcoin, Satoshi Nakamoto, must have realised this when he or she wrote the whitepaper. A Bitcoin address (to which you send coins) is a RIPEMD-160 hash of a SHA-256 hash of the elliptic curve public key. Importantly, this hash is not the same thing as the public key itself.
Why does this matter? It turns out that the hash offers a much stronger level of security than the elliptic curve:
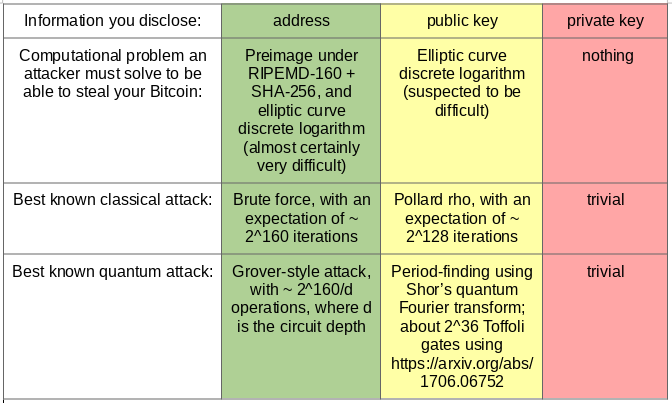
In particular, if an attacker knows only your Bitcoin address, then there’s no easier way for an attacker to steal your coins than by brute-force: generate a random private key, derive the public key, hash it to obtain an address, and see if it matches. It would take an expected 2^160 iterations of this approach to steal your coins.
Note that the attacker will almost certainly end up with a different private key from the one you created, but it will ‘coincidentally’ be able to unlock the coins in the same address. This is because the 160-bit space of addresses is 2^96 times smaller than the 256-bit space of elliptic curve keys.
What if an attacker knows your elliptic curve public key? Then, using the Pollard rho algorithm, it ‘only’ takes on the order of 2^128 iterations to determine your private key. That’s still humongous; even with all of the computing power currently available on the planet, it would take millions of years to reverse-engineer your private key.
So why should you be concerned? There are two reasons:
- There’s a polynomial-time quantum algorithm for breaking elliptic curve discrete logarithm. It uses the same ‘period-finding’ subroutine as Shor’s factorisation algorithm. It’s still far beyond current quantum computing technology, with the best published upper bound requiring 128 billion Toffoli gates to break a 256-bit elliptic curve discrete logarithm, but quantum computing progress has been accelerating in recent years.
- More of a concern is that Pollard’s rho algorithm might not be the best classical algorithm for solving the elliptic curve discrete logarithm problem. Prime factorisation, for example, became much easier as recently as 1996 when the General Number Field Sieve was invented (also by Pollard). It’s plausible that a secret governmental organisation has a faster method of cracking elliptic curve discrete logarithm.
If you’re unconvinced that this second reason is even remotely plausible, and strongly believe that Pollard rho is obviously the best possible algorithm for solving elliptic curve discrete logarithm, then you should ask yourself why serious cryptographers such as Joe Silverman are bothering to develop alternative methods.
(Before you dismiss this as an argumentum ad verecundiam, note that this is not purporting to be an argument that elliptic curve discrete logarithm is definitely insecure. Rather, it’s an argument that there’s no known proof that it is secure, because if such a proof did exist, then there would have been no point in Silverman proposing an approach that is guaranteed to fail.)
So, 2^128 iterations should be regarded as ‘an upper bound, which is tight assuming that there will be no academic, industrial, or governmental progress on finding faster algorithms’. And if a large-scale fault-tolerant quantum computer is developed, be very afraid…
On the other hand, cryptographic hash functions such as SHA-256 and RIPEMD-160 (both of which are composed to derive the Bitcoin address from the public key) are designed to thoroughly mush the input in as chaotic manner as possible*. They have no nice mathematical structure by design, so it’s very unlikely that there’s a better approach than the 2^160-iteration brute-force algorithm described above.
*that’s not to say that hash functions are just kitchen sinks of arbitrary operations. They’re still very carefully designed to have good dispersion properties, be resistant to a bunch of different cryptographic attacks, produce statistically random output, and achieve these goals efficiently (in terms of speed in software/hardware implementations).
The take-home message
To reiterate:
- if you share your public key, then your security level is “hopefully 128 bits, but maybe some organisation has found a faster method and is keeping it quiet”;
- if you don’t share your public key until you absolutely need to (when signing a transaction), then your security level is “almost definitely 160 bits”.
You should feel much more confident if your Bitcoin is in an address where the world doesn’t know your public key. This means that whenever you spend any Bitcoin from an address (inevitably revealing the public key in the process), you should empty the entire address and send the remaining balance to a fresh unused address.
You’re still revealing your public key, but only very briefly: as soon as the block containing that transaction is confirmed, it becomes incredibly computationally difficult to rewrite the history. In essence, it only gives an evil adversary a maximum of a few minutes to try to break the discrete logarithm problem.
Many wallet implementations create fresh addresses for every transaction, so my recommendation is to use one of those (e.g. the Trezor hardware wallet).
Since ‘not reusing addresses’ is already known to be best practice, then you might be tempted to ask:
Is this advice really necessary?
Apparently so.
At the time of writing, someone has 94258 Bitcoin* in a regular (pay-to-public-key-hash) address which has revealed its public key. So, if you are reading this and are the owner of 1P5ZEDWTKTFGxQjZphgWPQUpe554WKDfHQ, then I’d recommend moving the balance to a fresh address imminently.
*that’s about 3 billion dollars.
For example, if you look at one of the recent outgoing transactions, the ‘sigscript’ is the following:
473044022100ff4fa243701eea0bdba8615a8bc4f01df387 aae215a90fe382eaf5405ee0ad73021f6f814e02b88e1fbb 1b0d5099970da6cf426ef58027c4b99b1afb633bb5b62801 21024b83426cf9bff257261d87f2f2858b51b2eea756c0123c7e05bc0a007425c9f2
The last line here (68 hexadecimal characters, i.e. 34 bytes) contains 0x21 (meaning ’33’) followed by the 33-byte public key (a point on the elliptic curve). That is to say, there’s currently 3 billion dollars resting in an oft-reused Bitcoin address with an exposed public key, protected only by the difficulty of the elliptic curve discrete logarithm problem.
That’s a very large and unnecessary bet to be making against the collective innovative capability of the world’s algebraic geometers and cryptographers…
