The nth cyclotomic field is the field generated by a primitive nth root of unity, ζ. It is an example of a number field, consisting of algebraic numbers, and its dimension is φ(n) when regarded as a vector space over
. If n is odd, then the nth cyclotomic field is identical to the 2nth cyclotomic field, so we’ll henceforth assume without loss of generality that n is even.
The intersection of with the ring of algebraic integers is exactly the ring
generated by ζ. The first few examples of rings of this form are:
- n = 2:
, so
is just the ring of ordinary integers
.
- n = 4:
, so
is the ring of Gaussian integers (red, below-left).
- n = 6:
is the ring of Eisenstein integers (blue, below-right).
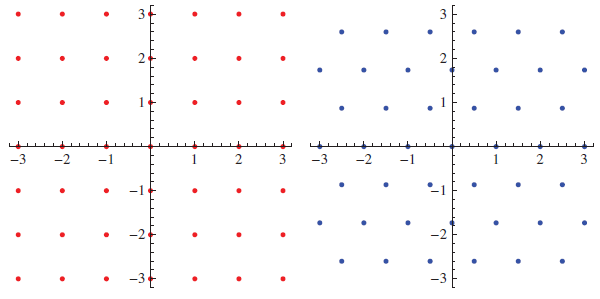
These three rings admit unique factorisation, meaning that every nonzero element can be uniquely expressed as a product of primes, up to reordering and unit migration. This turns out to be true for precisely the following thirty values of n:
2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 48, 50, 54, 60, 66, 70, 84, 90
The corresponding values of φ(n) are:
1, 2, 2, 4, 4, 4, 6, 8, 6, 8, 10, 8, 12, 12, 8, 16, 16, 12, 18, 16, 12, 20, 16, 20, 18, 16, 20, 24, 24, 24
Note that, in particular, the maximum dimension is φ(n) = 24, attained only by the three largest values of n (70, 84, and 90). These rings, viewed as additive groups, are therefore free Abelian groups of rank 24.
And this is where it gets exciting: David Madore noticed that the existence of order-70 and order-84 elements in the Conway group Co0 give rise to highly rotationally symmetric projections of the Leech lattice into the complex plane. Here’s the order-84 projection applied to the first shell:

Projection of the first shell of the Leech lattice into the plane with order-84 rotational symmetry, by David Madore
And here’s the order-70 counterpart:

Projection of the first shell of the Leech lattice into the plane with order-70 rotational symmetry, by David Madore
By suitably scaling and rotating either of these projections, we can arrange for the image to contain the respective nth roots of unity. If we view the resulting projection as a map from to
, we can see that it is surjective (because its image contains the roots of unity, and these span the field) and therefore bijective (because the dimensions match).
In particular, that means that the projection remains injective when restricted to the Leech lattice, and its image must be a rank-24 Abelian subgroup of which is closed under multiplication by roots of unity. Given that it has a finite integral basis, we can further scale/rotate the projection such that the images are all algebraic integers and therefore form an ideal in
.
Thanks to these rings having class number 1, every ideal is principal, so this ideal must simply be a scaled/rotated copy of itself! That is to say, when n is 70 or 84, we can identify the points in the Leech lattice with the algebraic integer elements of the cyclotomic field!
Working in the opposite direction, we can construct the Leech lattice starting from one of these cyclotomic fields by defining an inner product on its algebraic integer elements:
where α is a particular element of the ring (different choices yield different lattices), and tr is the trace operation (sum of all Galois conjugates).
There are similar constructions of the Leech lattice for some other values of n, where the class number is greater than 1 (and therefore unique factorisation does not apply), but the constructions could potentially require using a proper ideal rather than the whole ring of algebraic integer elements. For instance, Craig discovered a construction for n = 78, and Eva Bayer-Fluckiger gave a more thorough exploration.
The cases of n = 70 and n = 84 are arguably the most interesting, because they endow the Leech lattice with a compatible ring structure where unique factorisation holds: the nonzero lattice points form a multiplicative monoid isomorphic to the direct sum of a cyclic group of order n (the group of roots of unity) and the free commutative monoid on countably many generators.
Of these, the n = 84 ring is my favourite: it contains the Gaussian, Eisenstein, and Kleinian integers as subrings, and indeed is the smallest cyclotomic ring to do so.

Pingback: Cyclotomic fields and lattices – evin.one