Suppose that R is the (assumed to be finite) set of solutions to a certain problem, and you’re interested in determining the parity of |R|. The following proof strategy works surprisingly often, namely in at least two different scenarios, and leads to very elegant proofs:
- Embed R in a larger set S equipped with an involution f : S → S, such that R is precisely the set of fixed points of f;
- Define a second involution g : S → S, such that the set T of fixed points of g is easily seen to have the correct parity (usually by having 0 or 1 elements).
Then we have |R| = |S| = |T| (mod 2).
We’ll discuss two examples of this proof technique.
Example I: Zagier’s one-sentence proof
To prove Fermat’s theorem that every prime of the form 4k + 1 is expressible as the sum of two squares, Zagier famously provided the following ‘one-sentence proof’ discussed here:

Here, g is the complicated piecewise involution defined above, and f is the involution which interchanges the second and third coordinates. The set R is the set of ways to write , and the set U is the singleton set containing the fixed point of the complicated involution g.
Observe that this proof is constructive: you can use these involutions f and g to construct a solution to the original problem! Specifically, if you start at the (unique) element of U and alternately apply f and g, the other end of the path is an element of R:
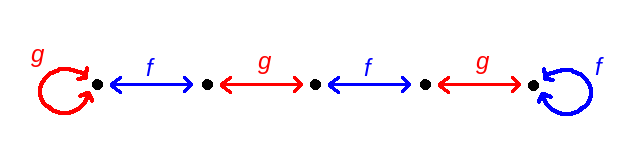
Christian Elsholtz similarly noticed this construction here albeit with the Greek letters α and β to refer to the two involutions.
At first, I though that this was a trick rather than a technique. In the words of Donald Knuth:
A trick is a clever idea that can be used once, while a technique is a mature trick that can be used at least twice.
That was until recently when I saw the following.
Example II: Hamiltonian cycles on cubic graphs
The problem is to show that, given a 3-regular graph G with a distinguished edge x, that there exists an even number of Hamiltonian cycles passing through x. Using this proof approach, we let:
- S be the set of proper 3-edge-colourings (with colours red, green, and blue) of the graph G such that x is assigned the colour blue;
- g be the involution that swaps red and green;
- f be the involution that swaps blue and green on every blue-green component other than the one containing the edge x.
The fixed points of f are those where the green and blue edges form a single (Hamiltonian) cycle. There are no fixed points of g, so U is the empty set. It follows, therefore, that |S| and |R| are also even.
Again, this proof is constructive: by alternately applying f and g, this gives you an explicit self-inverse way to transform any Hamiltonian cycle through x into a different Hamiltonian cycle through x:

This is a natural bijection, in that it doesn’t involve making any arbitrary choices such as labelling the vertices of G. Even better, it’s acceptable for constructivists since we can provide an explicit upper bound on the length of the path of alternating applications of f and g: it’s no longer than the size of S, which is in turn upper-bounded by 3^(3n/2); there are 3n/2 different edges, each of which is either red, green, or blue.
Anyway, does this technique have a name? If not, I’d propose ‘Zagiery’ after the discoverer of the first proof. And are there any other applications besides the two that we’ve looked at?

Mathologer’s video
“Why was this visual proof missed for 400 years? (Fermat’s two square theorem)”
https://youtu.be/DjI1NICfjOk
This reminds me of the following problem.
Given a group G, prove that the number of self inverse elements is either 1, even, or infinite.
If G is finite then the proof is easy (although it still took me a minute). You look at the elements which aren’t self inverse. There must be an even number since they pair up with their inverses. If there’s an order 2 element then the group must have even order, so by subtraction the number of self-inverse elements must also be even.
When G is infinite, you have to be a little cleverer. Here’s the proof I thought up.
Assume the number of self-inverse elements is finite, so that we want to prove it’s 1 or even. Take any self-inverse element. Then it acts on the other self-inverse elements by conjugation. This has some fixed points and involutes the rest of the points. So we want to prove there are an even number of fixed points. Pick any one of them different to the one we started with. Then since it commutes with the first element it acts on the fixed points by conjugation.
Continuing in this way we get a sequence of self-inverse elements that all commute. And since there are only finitely many self-inverse elements, this sequence eventually contains every self-inverse element that commutes with the rest of the elements in the sequence. So it forms a 2-group, hence its order is a power of 2. Then any number of the form 2^m + 2n is 1 or even.
I think this might be an example of your above proof technique, except iterated. The set of fixed points of g isn’t ‘easily seen to have the correct parity’, so we have to iterate with a g_1, g_2, etc., until we reach the empty set.
Yes, that’s definitely an example of what I had in mind. Elegant!
Are there other examples of proofs of existence by showing the number of solutions must have odd parity? Zagier’s proof seems to bypass the otherwise heavier machinery that would otherwise be needed, and I’m curious as to where else this can be exploited.
Yes, the proof of Sperner’s Lemma has this property: https://en.wikipedia.org/wiki/Sperner%27s_lemma#Proof
I don’t know the actual 1983 paper – but this quote from the pop-math book Shape by Ellenberg) “What Conway and Gordon really prove is that of the ten ways to partition the six points, the number that yield linked triangles is odd. But zero is even!” sounds like they establish existence (of a way to connect up 6 points in general position in 3-space to form two linked triangles) by establishing the parity is odd.
Required reading: Martin Aigner A Course in Enumeration.