EDIT (2021-10-14): I’ve written a reference implementation of the Hamming backup idea introduced in this article.
SeedXOR is an approach for splitting a Bitcoin wallet seed, adhering to the BIP39 standard, into N ‘parts’ (each the same size as the original) which are each a valid BIP39 seed. It is used by the COLDCARD wallet and preferred over more complicated Shamir secret sharing schemes on the basis that:
- the SeedXOR calculations are simple to do, such that they can be performed with pencil and paper without the aid of a computer;
- each of the N parts of a SeedXOR backup is itself a valid BIP39 seed, so they can contain ‘decoy wallets’ and thereby steganographically hide the fact that they’re even part of a SeedXOR backup at all!
On the other hand, Shamir secret sharing enables ‘M-of-N’ backups, where only M parts are necessary to reconstruct the original seed (instead of all N parts).
Here we present a ‘2-of-3’ variant of SeedXOR which retains many of the desirable properties of the original SeedXOR:
- the seed X is used to construct three ‘parts’ (each the same size as the original seed, as in SeedXOR), called A, B, and C;
- as in SeedXOR, each of these three parts is indistinguishable from a standard BIP39 seed (giving rise to plausible deniability);
- this is backwards-compatible with SeedXOR, in that if you have all three parts, then you can reconstruct X by simply taking A ⊕ B ⊕ C (and recomputing the checksum);
However, unlike a regular SeedXOR backup, this modified variant allows for full recovery of the original seed even when one of the three parts is missing:
- given any two of the three parts, the seed X can be recovered.
This new variant is called a ‘Hamming backup‘ because the construction is based on an extended Hamming code. Generating a Hamming backup and recovering a seed from a Hamming backup can be done using only the XOR operation, as with SeedXOR. It’s slightly more complicated than SeedXOR in its construction (which is inevitable, because this implements a 2-of-3 scheme instead of an N-of-N scheme), but still possible to do with pencil and paper using only the XOR operation.
In particular, we firstly regard the 256-bit seed X as the union of two 128-bit values, X1 and X2, and similarly regard the parts A, B, and C as the unions A1+A2, B1+B2, C1+C2. We’ll explain later how to split a BIP39 seed in this manner.
The linear (bitwise XOR) relations that we impose between the different 128-bit values are summarised in the following diagram. (The analogous diagram for ordinary SeedXOR would be a single circle containing N+1 values, namely the seed X together with the N parts A, B, …)
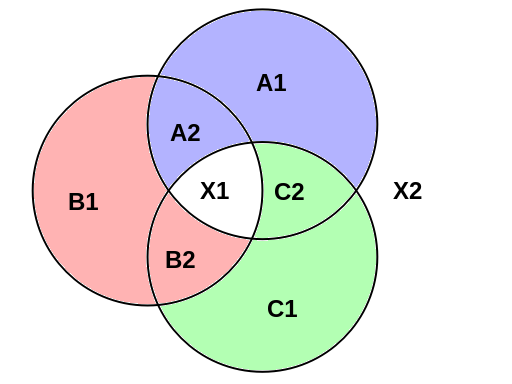
This diagram has three circles, each of which has 4 values inside (in the case of the top-right circle, these are A1, A2, X1, C2) and 4 values outside (in this case, B1, B2, C1, X2). If four values are either all inside the same circle or all outside the same circle, then we impose the relation that they all must bitwise-XOR to zero. For example:
- A1 ⊕ A2 ⊕ X1 ⊕ C2 = 0
- B1 ⊕ B2 ⊕ C1 ⊕ X2 = 0
and analogously for the other two circles:
- B1 ⊕ B2 ⊕ X1 ⊕ A2 = 0
- C1 ⊕ C2 ⊕ A1 ⊕ X2 = 0
- C1 ⊕ C2 ⊕ X1 ⊕ B2 = 0
- A1 ⊕ A2 ⊕ B1 ⊕ X2 = 0
Equivalently, for each of these quartets, any one of the four values is given by the bitwise XOR of the other three.
Further linear relations can be derived from combining existing relations; for example, X1 = A1 ⊕ B1 ⊕ C1 and X2 = A2 ⊕ B2 ⊕ C2. Indeed, there is a group-like closure property: if you take any 3 of the 8 values in the diagram and bitwise-XOR them together, the result of the calculation is one of the 8 original values.
We’ll now discuss how these relations enable the seed X to be recovered from any two of the three parts {A,B,C} of a Hamming backup. Then we’ll discuss how to actually produce a Hamming backup {A,B,C} from an existing seed X together with a source of secure randomness (specifically, by generating A randomly and then deterministically deriving B and C from A and X).
Recovering a seed from a Hamming backup
The relations have the property that, given parts A and B, we can recover the seed X as follows:
- X1 = A2 ⊕ B1 ⊕ B2 (they’re all inside the left circle)
- X2 = A1 ⊕ A2 ⊕ B1 (they’re all outside the lower-right circle)
This can be done in three applications of XOR, rather than four, by precomputing the common subexpression A2 ⊕ B1. As such, this is only 50% slower than recovering a seed from a 2-of-2 SeedXOR backup, rather than twice as slow.
Moreover, the whole diagram has order-3 cyclic symmetry, so you can do the same thing with parts B and C, or with parts C and A. That is to say, you can recover the original seed with any two of the three parts.
Important note: when using two parts to generate the seed X, it is important that the two parts are used in the correct order (swapping the roles of A and B, for instance, would result in us generating the remaining part C instead of the desired secret X). If we made this mistake (and recovered C instead of X), then X can be derived by straightforwardly XORing together A, B, and C.
Constructing a Hamming backup
How does one construct a Hamming backup of an existing seed X? The first part, A, should be securely uniformly randomly generated. This will ensure that no information about X is leaked to an attacker who possesses only one of the parts {A, B, C}. (Like SeedXOR, one-time pads, and Shamir secret sharing, this is an information-theoretically secure construction, rather than a construction that depends upon the computational intractability of some problem.)
The remaining parts of the backup can be derived by moving anticlockwise around the diagram, obtaining each value from the XORing the previous two (in cyclic order around the diagram) together with one of the values from the seed X. Specifically, we compute:
- B1 = A1 ⊕ A2 ⊕ X2;
- B2 = A2 ⊕ B1 ⊕ X1;
- C1 = B1 ⊕ B2 ⊕ X2;
- C2 = B2 ⊕ C1 ⊕ X1;
- A1 = C1 ⊕ C2 ⊕ X2;
- A2 = C2 ⊕ A1 ⊕ X1;
The last two lines here are redundant — they compute the values A1 and A2 with which we already started — but are useful as a validity check in case you made errors whilst computing B1, B2, C1, and C2. An independent check is to load {A,B,C} into a COLDCARD hardware wallet, pretending that it’s a regular 3-of-3 SeedXOR. If the Hamming backup has been created correctly, this should load the original seed X = A ⊕ B ⊕ C.
BIP39-friendly way to split X into X1 and X2
If we only cared about the machine implementation of Hamming backups, then it would be straightforward to split the 256-bit value X (i.e. the entropy part of the seed, with no checksum) into an initial 128-bit segment and a final 128-bit segment.
However, part of the reason for favouring SeedXOR and Hamming backups over more complicated Shamir schemes is the ability to perform the calculations relatively quickly using pencil and paper without the aid of a computer.
The BIP39 standard appends an 8-bit checksum to the 256-bit seed (to create a 264-bit value) and then splits it into 24 words of 11 bits:
- word 1: [11 seed bits]
- word 2: [11 seed bits]
- word 3: [11 seed bits]
- […]
- word 23: [11 seed bits]
- word 24: [3 seed bits + 8 checksum bits]
These are each represented either as English words (from a 2048-element wordlist) or as 3-digit hexadecimal numbers where the first digit encodes 3 bits and the other two digits each encode 4 bits, making up the total of 11.
The hexadecimal representation is used when computing SeedXOR manually; a 16×16 lookup table is provided for applying the bitwise XOR operation to hexadecimal digits.
So that Hamming backups can be conveniently computed using the same mechanisms used by ordinary SeedXOR, we propose splitting the 24-word seed X into the 128-bit components X1, X2 as follows:
- X1 contains words 1–11 followed by the first two hex digits of word 12;
- X2 contains words 13–23 followed by the first hex digit of word 24 and the third hex digit of word 12.
On paper, we would write the hexadecimal digits of X1 directly above those of X2, like so:
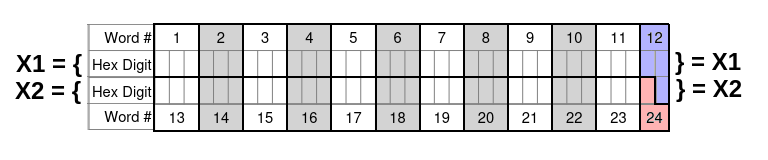
Observe that only the first hex digit of word 24 is included (since the other two are checksum digits). Also, the first two digits of word 12 contribute to X1, whereas the third digit contributes to X2.
Crucially, the hex digits in the seed have been arranged into the two rows in such a way that each 4-bit digit in the X1 row appears above a 4-bit digit in the X2 row, and each 3-bit digit in the X1 row appears above a 3-bit digit in the X2 row. This means that performing bitwise XOR operations between different rows doesn’t ever yield an invalid value (such as causing the first hexadecimal digit in a word to be 9, which is outside the valid range 0..7).
Relationship with Shamir secret sharing
Hamming backups are isomorphic to a special case of Shamir secret sharing, where the degree of the polynomial is 1 (so it’s a 2-of-N scheme) and the construction operates over the field GF(2^2) of four elements. The three parts {A,B,C} encode the value of the polynomial evaluated at the three nonzero elements of the field, {1,ω,ω+1}, and the seed X encodes the value of the polynomial evaluated at 0.
Since we’re only dealing with a degree-1 polynomial, this construction is linear (which is why we were able to implement it exclusively using XOR). Shamir schemes based on higher-degree polynomials are not amenable to this technique, so do not give rise to arbitrary M-of-N analogues of Hamming backups.
The fact that Hamming backups only offer a 2-of-3 scheme is a limitation compared with the arbitrary M-of-N schemes possible with general Shamir secret sharing. It may be possible to implement M-of-N schemes using more sophisticated binary error-correcting codes, but doing so entails further sacrificing the simplicity of the original SeedXOR scheme.

Does it make sense to repeat the process?
Split X => X1, X2. Generate A1, A2, B1, B2, C1, C2.
Combine unmatched halves: A1+B2 => AB, B1+C2 => BC, C1+A2 => CA.
Split AB => AB1, AB2. Generate D1, D2, E1, E2, F1, F2.
Repeat for BC, CA.
You now have 9 parts instead of only 3, and you need four of nine to recover X.
Problems I see:
1. Step 3 can’t just break AB the same way that A and B were broken, otherwise AB1 would be the same as A1 and AB2 would be the same as B2. A more complicated hex mixing would need to take place.
2. Also the BIP39 checksums would be broken by combining unmatched halves, unless more correction is done in step 2.