Robin Houston, Nathaniel Johnston, and I have established some new bounds on the tensor rank of the determinant over various fields. The paper is now available as an arXiv preprint and contains the following results:
- A new formula for the determinant (Houston’s identity) which applies over arbitrary commutative rings and establishes an upper bound of the nth Bell number for the tensor rank of the n × n determinant. This is a superexponential improvement over the previous state-of-the-art, which was
- Tighter upper bounds in fields of characteristic p using the same identity, including an upper bound of
in characteristic 2.
- Two completely independent proofs of Houston’s identity: a combinatorial proof (which is a more streamlined version of the proof from this cp4space post) and a geometric proof.
- Mildly improved lower bounds on the tensor rank of the determinant (improving Derksen’s bound by a small additive term).
- A computer-assisted proof that the tensor rank of the 4 × 4 determinant over the field of two elements is exactly 12, which consumed 357 core-hours of CPU time*.
- Some geometrical motivation which relates the formula to an interesting tiling of axis-aligned polytopes, the 1-skeleton of which is interpretable as a flip graph for ordered partial partitions:
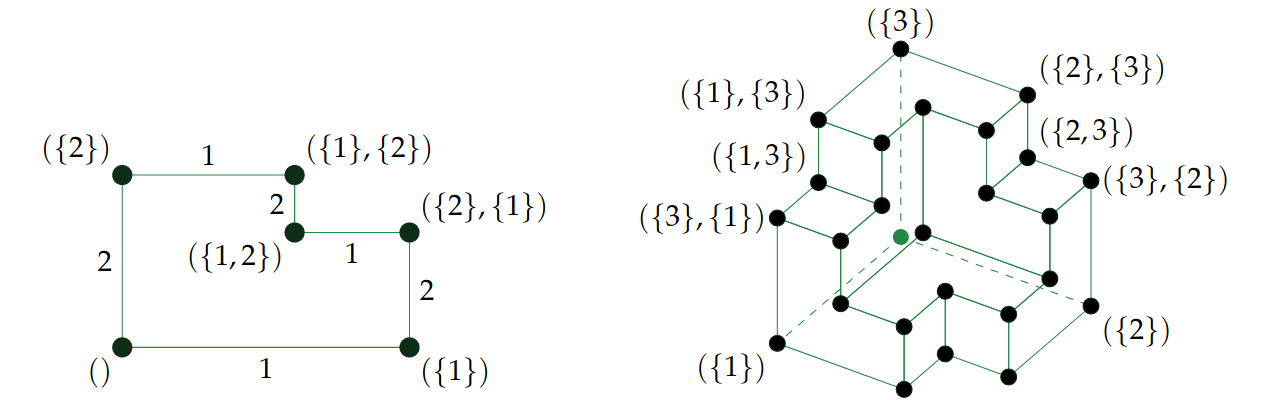
David Eppstein talks more about orthogonal polyhedra here.
*the same machine later found the Walrus, the first (and currently only known) example of an elementary c/8 diagonal spaceship in Conway’s Game of Life.
