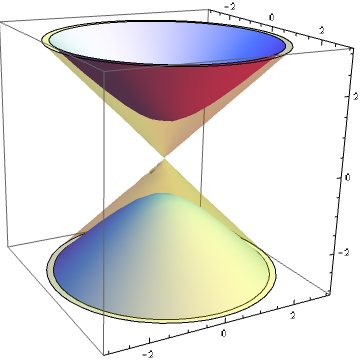
At the moment, assuming everything has gone according to plan, I should currently be on a northward-bound train, returning from Kevin Buzzard’s talk at the Royal Society.
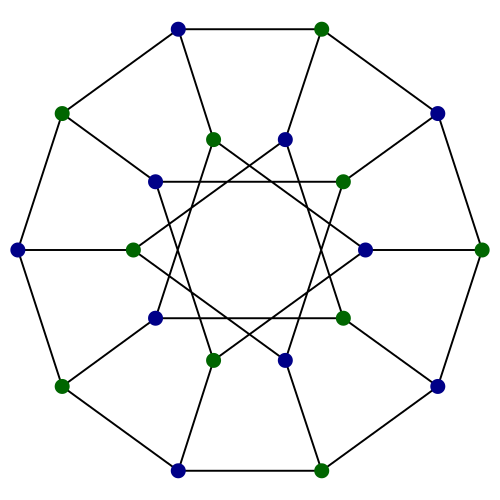
As with some of the earlier ciphers, this is bipartite, consisting of both an image and a block of ciphertext. Firstly, the image:

And now the ciphertext:
{"001001110", "011111000", "111111101", "011100100", "101011110",
"010001110", "000101101", "111101111", "100000101", "100100000",
"111101111", "010001011", "000011011", "111101101", "010000010",
"001000110", "001000101", "011101110", "000000000", "000001010",
"111010000", "110111010", "101010010", "000011110", "101110100",
"110100010", "111000010", "000101101", "110000100", "011111100",
"101010010", "100000010", "111010010", "101011010", "101111111",
"111100001", "101000000", "011110101", "011000100", "110110000",
"000010010", "101010011", "010010111", "011010010", "001111110",
"010001011", "110000000", "000111011", "010100010", "001000010",
"001001101", "111111011", "000110111", "010011011", "001000101",
"111100001", "000011110", "100111110", "010001111", "111100001",
"111011111", "010001011", "010010101", "110100001", "010011101",
"000011110", "100011101", "111101000", "111011101", "001011011",
"011100010", "000101110", "101110001", "101110100", "000001000",
"100000110", "100000100", "001011110", "101111100", "100001011",
"011100010", "010110101", "101111011", "101110010", "000010010",
"101001001", "100011011", "010100000", "110000100", "011000010",
"010011110", "110001010", "101101110", "111101000", "100010001",
"011010011", "100010110", "010100000", "010001010", "011000101",
"000000011", "100100001", "011110010", "100100010", "100010010",
"010100011", "000101111", "110100100", "001001110", "101110000",
"001000001", "011010110", "010001011", "100100010", "010101101",
"100111110", "100001010", "001000000", "100000100", "001111011",
"000011101", "011000100", "010000001", "101001010", "011000001",
"000000101", "010010111", "010100010", "110000010", "101000101",
"111100100", "001101100", "101100010", "010100010", "001000011",
"110111111", "110000001", "010010111", "000000010", "110000101",
"010000000", "101011100", "101000100", "100000001", "100010101",
"010100011", "110111100", "000111110", "001001110", "111000010",
"110111111", "111110000", "011000010", "010000110", "011101001",
"001110101", "000100001", "101011110", "111011110", "010010101",
"100001011", "110000000", "000011111", "011101110", "000000000",
"100000000", "110110010", "100001111", "001111101", "110000001",
"010010000", "010000000", "010000000", "011101000", "110111100",
"000101101", "011100010", "111101000", "100001001", "110111110",
"000110111", "100000110", "101011001", "110111101", "001000101",
"010001010", "010010110", "001111011", "001011110", "101100100",
"000100111", "110000010", "110111100", "010001111", "111010000",
"110100010", "011011110", "111111001", "000010111", "101111010",
"000100001", "100100000", "111110000", "001001011", "111111101",
"010100010", "010000110", "010000001", "101010001", "010000001",
"011000010", "101010110", "101100100", "110110100", "111101110",
"110111100", "010001110", "011110010", "100111110", "101100100",
"000000110", "010001000", "100001011", "111101111", "010111110",
"000011011", "001110101", "000100000", "011000100", "010100000",
"100010111", "110000011", "110111001", "111100010", "101110111",
"010000111", "100000011", "010010110", "110111101", "101100100",
"100100010", "110000100", "101000100", "101101110", "010001101",
"011000001", "000100000", "110010011", "010010000", "011000010",
"000101011", "011101010", "101101101", "110110100", "010000001",
"010100011", "111110000", "101110000", "001000001", "000000101",
"110100001", "001101010", "000001001", "011101110", "010001001",
"010110110", "010000110", "001111001", "000010010", "011010110",
"100001000", "010111001", "101000010", "010010001", "011100001",
"000101111", "001011110", "100011011", "100011011", "011110010",
"000000100", "110000000", "001011110", "110001010", "101011111",
"010010101", "000100111", "101101001", "010111110", "101101001",
"010010000", "001000001", "010010110", "111001000", "111110111",
"101101000", "000011111", "000001000", "011000000", "110010011",
"110000001", "010100011", "101000100", "110000001", "100100001",
"101111110", "001000001", "010110110", "010000101", "100101001",
"101111001", "001001110", "000111011", "011110100", "111011101",
"010010110", "110110000", "001001111", "101111000", "111011000",
"110000000", "100111011", "011110000", "100001000", "010001001",
"001000011", "100010010", "011011001", "011111111", "000111101",
"010111111", "101101110", "101111101", "010011110", "001000111",
"111000001", "010000111", "111101101", "110000001", "001000110",
"100001101", "111011000", "001111011", "011110100", "110000000",
"110000101", "100100000", "000000110", "101100100", "100111010",
"000100000", "101011101", "001001011", "001111110", "010010110",
"001111111", "001001101", "110010011", "111100000", "100001111",
"100001111", "000000010", "000000101", "001110101", "010010010",
"010000100", "110111111", "100011011", "001010111", "101111101",
"000010001", "011000010", "010011101", "000011110", "111100100",
"111100100", "110100100", "101011001", "010011011", "100000000",
"001000010", "110000101", "010000100", "010110110", "010111110",
"000101101", "100100010", "100010101", "100011101", "111010010",
"000100000", "110111111", "100000001", "011010010", "111010100",
"011000001", "011000001", "101010101"}
compared with 2 last year and 1 in the inaugural year) are partially a result of the wider dispersion of this exam, and highlights that the previous machinery* for selecting candidates may have been suboptimal. However, the proportion of schools entering this competition was not particularly large, so we can still do even better…