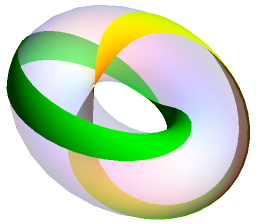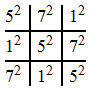Complex Projective 4-Space

The torus is a reasonably interesting object. It can be embedded in as a quartic surface bounding a doughnut, or obtained by identifying opposite edges of a square. An intermediate between these constructions is the Clifford torus, which is the Cartesian product of two circles.

On the sphere, the Schönflies theorem (related to the Jordan curve theorem) tells us that any closed curve splits the surface into two components, each of which is homeomorphic to the disc. Obviously, this is not true on the torus: removing a small disc from the surface gives a surface which is not simply connected, and therefore not homeomorphic to the unit disc. More surprisingly, it is possible to remove a closed curve without creating two disjoint components. Indeed, this enables two linked loops to be drawn on a torus:

I had intuitively assumed that this was impossible (it’s hard to visualise until you see the diagram above), which caused great confusion when I read that the Petersen graph is toroidal but not linklessly embeddable. Even more impressively, the trefoil knot can be drawn on the surface of a torus:

For obvious reasons, it is known as a torus knot. Torus knots can be obtained by drawing a line of rational slope on a unit square and identifying pairs of opposite edges. The trefoil knot corresponds to the rational 3/2. Similarly, the rational 5/2 gives rise to the cinquefoil knot.

If we choose an irrational number instead, then we get an injection from the real line to a torus. For instance, here is the image of [0, 100] using the irrational number φ.

The image of the real line is a dense subset of the torus, and serves as a good counter-example for disproving certain false statements in topology.

Some proofs of existence provide explicit examples. For instance, a proof of a composite Fermat number is as simple as noting that . On the other hand, some existence proofs are highly non-constructive, and do not provide explicit examples. The proof that the reals can be well ordered cannot be realised as a constructive proof, since the statement is independent of the Zermelo-Fraenkel axioms.

In this post, we’ll consider the borderline between constructive and non-constructive proofs. I have provided four examples, which vary in terms of constructiveness.

Gardens of Eden

A pattern in Conway’s Game of Life is known as a Garden of Eden if it cannot arise within the successor of another pattern. The proof of the existence of Gardens of Eden relies on the non-injectivity of the rules; two patterns (such as those below) are mapped to the same pattern (namely the one on the left):

Now, consider a general pattern. There are 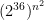possible patterns of this size, but at most A = are non-equivalent. The total number of patterns in a 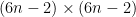box is B = 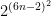. As every box determines a  box in the following generation, at most A patterns in a box of side length are actually constructible.

If we choose n sufficiently large so as to ensure that A < B, then there must exist a Garden of Eden. By writing down the inequality and manipulating it, one can deduce an upper bound of 6859110463024 for the side length of the minimal Garden of Eden. One ‘explicit example’ is the lexicographically first Garden of Eden of this size. A more explicit example is the concatenation of all patterns of this size, which must itself be a Garden of Eden by virtue of containing one.

Of course, this argument is pretty pointless as a completely explicit example, which inhabits a 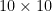box, has already been found.

Primes with one billion digits

There’s currently a substantial prize offered by the Electronic Frontier Foundation to discover a prime with one billion decimal digits. Due to Bertrand’s postulate, we can be sure that such a prime exists; it is located between 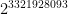and . Hence, we can provide an ‘explicit’ example of a prime with one billion digits, namely the largest prime factor of . However, this seems to be ‘cheating’, and would obviously not win the EFF prize.

Primitive roots modulo infinitely many primes

An integer n is described as a primitive root modulo p if every number in 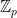can be expressed as some power of n. For instance, 3 is a primitive root modulo 7, whereas 2 is not. Dr Roger Heath-Brown demonstrated that at most two non-square integers are not primitive roots modulo infinitely many primes. Nevertheless, no numbers have yet been proved to be primitive roots modulo infinitely many primes. So, we know that at least one integer in the set {2, 3, 5} is a primitive root modulo infinitely many primes, and we can take ‘the smallest one satisfying this property’ to be our ‘explicit example’.

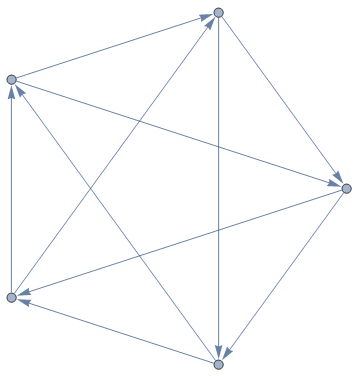
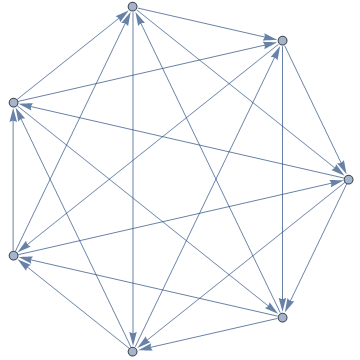
Obstruction sets for toroidal graphs

Wagner’s theorem states that a graph is non-planar if and only if it contains either the complete graph K5 or the bipartite graph K3,3 as a graph minor. The Robertson-Seymour theorem implies that we can find a similar obstruction set for toroidal graphs (graphs that can be drawn on a torus without edges crossing), but we have no idea how large such a set could be.

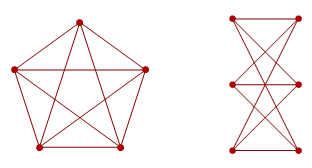
It’s possible, however, to inject the finite sets of graphs into the positive integers. I’ll leave this as an exercise to the reader; it’s not too difficult. Consequently, out of all valid obstruction sets for toroidal graphs, we can choose the one corresponding to the smallest integer. This is still an explicit example in some sense, but even less so than the other examples I’ve provided (there are no size bounds).

If you’ve been affected by any of the issues in this article, please discuss them here in the ‘comments’ section at the foot of the page. In particular, I would like to hear your views on where you draw the line between explicit examples and non-constructive proofs.

In an earlier cp4space post, I presented a set of five 5-sided dice. We can draw a directed graph associated with this set of dice:

Each vertex represents a die. If die A beats die B with a probability greater than ½, we draw a directed edge from A to B. If two dice have equal probability of beating each other, we leave the edge blank. We make the additional restriction that for each value x, no two dice can have x on a face; this ensures that there are no ‘draws’ between two dice.

Can we, for every directed graph, create a set of non-transitive dice corresponding to it? Radu Bumbacea answered this question in the affirmative, devising a construction for a set of n dice with 2e faces emulating any given digraph with n vertices and e directed edges. So, for the digraph given above, his construction would require five icosahedral dice. You might want to try finding a similar construction yourself.

Tournaments, lower bounds and quadratic residues

A tournament is a complete directed graph with n vertices and edges. Radu’s construction gives an upper bound of faces on each die. Can we establish a lower bound? Indeed, we can. There are different tournaments on n vertices, and ways to assign distinct values to n dice with F faces each. Using Stirling’s formula and considering the asymptotics, it is evident that we have a lower bound of , where the logarithm is base-2. This is considerably lower than Radu’s upper bound.

In the basic set of three non-transitive dice, we have the property that if one player chooses a die, you can choose another die so that you have a probability greater than ½ of securing a win. We can choose a more complicated tournament, where any pair of dice can be beaten by a third die. An elegant solution is to consider the dice to be integers modulo 7, and declare that one die beats another if their difference is a quadratic residue:

Using Radu’s construction, we can design a set of seven 42-faced dice which beat each other according to this directed graph. It transpires that this is quite suboptimal, though, as Oskar van Deventer discovered an equivalent set of seven 3-faced dice; their double covers are shown below:

The quadratic residue construction also gives a tournament with 19 vertices, where any set of three vertices is beaten by another vertex. Oskar hasn’t found an elegant set of dice for this tournament, although Radu’s construction gives a set of nineteen 342-faced dice. The order-19 tournament is rendered below, where the colour gradient indicates edge direction:

It’s possible to generalise even further, constructing sets of dice such that for any subset of size k, there exists a die which beats each of them with probability ≥ ½.

In 1770, Leonhard Euler sent this particular curiosity to Joseph Lagrange. It’s a 4-by-4 magic square, all of whose entries are perfect squares.

Martin Gardner offered a prize for finding a 3-by-3 magic square of squares. Lee Sallows found a weaker version where all rows, columns and one of the diagonals have the same sum, but no-one has found either an example or a proof of the non-existence of fully magic squares of squares. If we relax the condition that all entries are distinct, the problem becomes trivial:

These trivial examples correspond to solutions of the Diophantine equation , which are in turn equivalent to rational points on the circle with radius . Once you have one solution (such as ), then it is possible to find all of the solutions by considering lines of rational slope passing through this point.

If we allow larger magic squares, there exist magic squares which remain magic when every element is squared. These are known as bimagic squares, the smallest known example having a side length of 8, a sum of 260 and a sum of squares of 11180.

Returning to the original problem of finding a 3-by-3 magic square of squares, it is not too difficult to demonstrate equivalence to the problem of solving a bunch of simultaneous quadratic Diophantine equations. Another problem that can be stated in this form is the difficulty of finding a perfect cuboid: does there exist a cuboid such that every pair of vertices has an integer distance of separation?

A group* of twelve of us congregated in London to mark† the second round of the British Mathematical Olympiad. After several hours of marking, punctuated with a surprisingly high-quality lunch, we were able to announce the scores. The high scores are available on the BMOC website; well done to everyone who featured!

Additionally, we had the equally difficult task of deciding between many extremely competent mathematicians to select the teams for the Romanian Masters of Mathematics and the European Girls’ Mathematical Olympiad. I wish the best of luck to the new teams in these forthcoming international competitions.

Footnotes (mainly for the pedantic reader)

* Precisely half of us commuted together on the Cambridge-to-London train. The rest, however, did not, so we can’t claim to be Abelian.

† Upon re-reading this, I realise that the word ‘mark’ in this context is semantically ambiguous and could be interpreted as ‘commemorate’. I shall clarify that in this case, ‘marking’ refers to the practice of scrutinising submissions, evaluating them and assigning numerical scores based on the validity of the proofs.

Langton’s ant is a two-dimensional generalisation of a Turing machine, known as a turmite (a portmanteau of ‘Turing’ and ‘mite’, as well as being a pun on ‘termite’), renowned for its simple rules and interesting behaviour. Specifically, it has one state and two colours, and obeys the following rules:

• If the ant is on a white square, turn right and paint the square black;
• If the ant is on a black square, turn left and paint the square white.

The behaviour for the first 200 steps is shown in this animation:

It transpires that in about 10000 steps, the ant’s behaviour becomes periodic, building a diagonal highway ad infinitum. It has been proved that no initial configuration can lead to a bounded (cyclic) route, but it is unknown as to whether there are other attractors as well as the simple highway.

The 349th problem on Project Euler asks how many black squares are produced in 10^18 steps. This can be done with a little work once the periodic behaviour is known. However, we’re too lazy to actually do the relevant periodicity checking and linear extrapolation, so we’ll instead employ a minimal-effort solution:

1. Run the cellular automaton program Golly, and open ‘Patterns/Other-Rules/Langtons-ant.rle’.
2. Execute ‘goto.py’ and enter ‘1000000000000000000’ into the dialogue box.
3. Press the ‘enter’ button and wait less than one second for the miracle of the HashLife algorithm to simulate all 10^18 generations.
4. Read off the population count, and adjust according to whether the ant is on a white or black square.

(I’m not going to give the numerical value here, as that would be a spoiler for anyone who wants to solve the problem legitimately.)

Some of the earlier problems on Project Euler have one-line solutions in Mathematica, but this is probably the ‘hardest’ problem to be trivialised by possessing powerful software.

Tim’s turmite challenge

If we allow the two-dimensional Turing machine to have two states instead of one, there is an explosion of rich and complicated behaviour. Ed Pegg asked for the one which lasts the longest before becoming predictable (Langton’s ant, taking 10000 generations, is a weak lower bound).

Shown above is a 2-state machine which takes over 4 million steps before settling into a periodic cycle. Since then, the record has been smashed twice in a short space of time, with the current winner taking 240 million generations of chaotic behaviour before finally building two highways in opposite directions:

Zoomed-out image of the final state of Georgi Gochev’s 240-million-step turmite

Tim Hutton and Ed Pegg have set the challenge of finding turmites with longer stabilisation times, encouraging a distributed effort. If you’re interested, follow the instructions on the relevant page.

A positive integer N is described as a perfect number if the sum of all of its proper divisors (that is to say, factors of N other than N) is equal to itself. For instance, the proper divisors of 28 are 1, 2, 4, 7 and 14, which sum to 28.

The first few perfect numbers are {6, 28, 496, 8128, 33550336, …}. Since 2008, the largest known perfect number was . This record has now been broken, with the discovery of the perfect number .

It is unknown as to whether there are any odd perfect numbers. An even number is perfect if and only if it is of the form , where is a (Mersenne) prime. Mersenne primes are much easier to verify than ordinary primes of similar size; the Mersenne prime can be verified in time by using the Lucas-Lehmer test together with the Schönhage-Strassen algorithm for multiplying large integers. By comparison, a non-Mersenne prime of a similar size takes time using the best known algorithm (AKS) for primality testing.

As of today, there are now 48 known perfect numbers. We don’t know whether there are any more, although it has been conjectured that there are infinitely many.