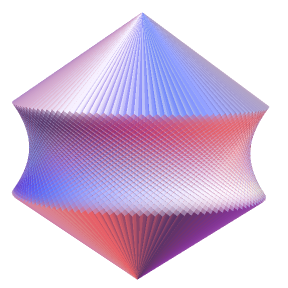
Suppose we took a solid unit cube and balanced it on a vertex. Next, we spin the cube really quickly about the vertical axis, producing a solid of revolution:
Clearly, the top and bottom are two identical cones produced by revolving a line segment passing through the axis of rotation. What about the thing between them? It is a quadric surface (three-dimensional conic) called a hyperboloid of one sheet. Alas, this name invariably reminds me of a television commercial for a particular brand of kitchen towels:
[youtube=http://www.youtube.com/watch?v=Xknub_pILt8]
The hyperboloid of one sheet is a doubly ruled surface, meaning that at each point we can find two straight lines drawn on the surface of the hyperboloid which pass through the point*. The only other doubly ruled surfaces are the plane and hyperbolic paraboloid.
* Proof: The hyperboloid is the surface swept out when one of the edges of the cube is revolved about the axis, so must be at least singly ruled. However, the hyperboloid possesses bilateral symmetry, so we can find a second family of lines by reflecting the first family.
One may ask what the volume of the revolved cube is. After some pretty easy stuff involving Pythagoras and vectors, we obtain the various dimensions of the cross-section of the revolved cube:
The two cones each have volume (2 sqrt(3)/27)π, and the hyperboloid has the Cartesian equation 2x²+ 2y² – 4z² = 1, where the centre of the cube is the origin. Basic integration gives a volume of (5 sqrt(3)/27)π for the hyperboloid, so the entire solid has volume π/sqrt(3). It is interesting to note that this total volume, which was obtained in a very piecewise manner, is simpler than the volumes of its conical and hyperbolic components.


You have no idea for how long I was thinking about this problem! My only conclusions were that rotated cube creates 2 cones and curved surface, probably with negative curvature. And suddenly, in great detail, someone explains that with exact measures. I believe your calculatios are correct, though I’m not into double integrals, but thanks so much anyway!
Oh, I’m glad that you found this helpful.
You don’t need to use a double integral for volumes of revolution. A single integral will suffice if you use cylindrical polar coordinates (the most natural coordinates to use here). The formula for a volume of revolution is pi*Integrate(r^2 dz), where r (radius) is a function of z (height).
The volumes of the cones are quite easy to determine, and I verified that the volume of the hyperboloid is slightly less than (specifically, 5/6 of) that of the enclosing cylinder. So, the calculations were indeed probably correct.
Pingback: 27 lines on a cubic | Complex Projective 4-Space
I wonder what the area of the 2d shape that would revolve around the y-axis to get the solid?
I too was thinking about revolving a cube around two of its opposing corners, but could not find a program that would qualify to create such a shape. May I ask what did you use to create the above shown image?