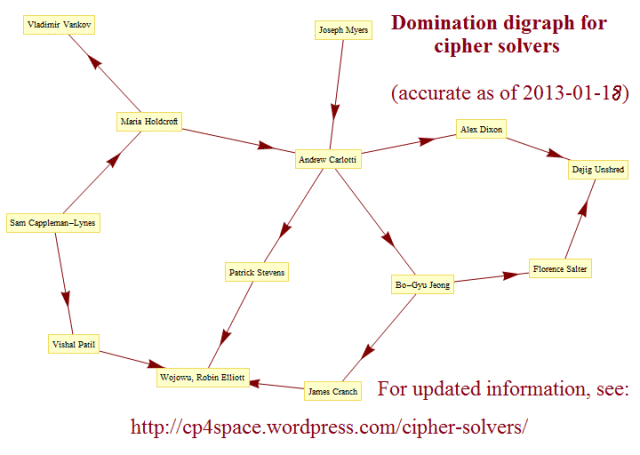
Suppose we have a set of n people, and we want to encapsulate a particular relation which holds between them. For instance, the people who have featured on the cipher solvers page can be represented by a directed acyclic graph. We have a directed edge A → B if person A dominates person B, that is to say that A solved a proper superset of the ciphers solved by B. There is also the transitivity property: A → B and B → C together imply A → C. I have removed these extraneous edges from the digraph to improve clarity.
Sam Cappleman-Lynes and Joseph Myers are known as maximal elements, as no-one dominates either of them. The entire graph is an example of a partially ordered set, or poset.
For more symmetrical relationships, it is better to use an undirected graph. For instance, we can connect two people (vertices) with an edge if they are friends with each other. There is no convenient way to analyse the entire global friendship graph, although social networks provide good approximations. There has been a paper examining this graph and revealing certain interesting properties; for instance, the largest connected component of a particular network features about 700 million people, whereas the second largest contains roughly 2000 people.
From graphs to hypergraphs
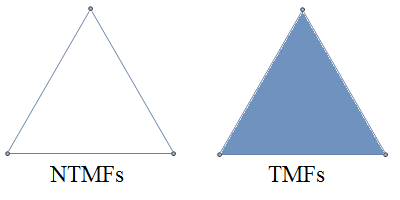
Vishal Patil and I realised that an ordinary graph is insufficient to embody certain concepts in social communities. For instance, if A, B and C are mutual friends, they would be represented by the cycle graph C_3. However, we can make a more subtle distinction: do the three people know each other merely pairwise, or have they all met simultaneously? By using something called a hypergraph, we can distinguish between non-trivial and trivial mutual friends:
Trivial mutual friends are far more common, and are just three people who know each other having been together simultaneously. Non-trivial mutual friends (NTMFs, a term originally coined by Vishal, which has later passed into widespread use) are much rarer; the canonical example provided by Vishal was that someone he met at school later encountered James Aaronson on a tour of Israel. An analogy is that 6, 10 and 15 are pairwise non-coprime, but are coprime when considered together.
The set of hypergraphs which can arise is far smaller than the powerset of the powerset of the number of people. In particular, certain constraints must be obeyed:
- If A is an element of the hypergraph, and B is a subset of A, then B is also an element of the hypergraph (obviously);
- For every vertex v, the singleton set {v} belongs to the hypergraph (people vacuously know themselves).
Hypergraphs obeying this restriction are known as abstract simplicial complexes. The number of abstract simplicial complexes on n labelled vertices is given by {1, 2, 9, 114, …} (sequence A006126 in the OEIS). Equipped with this new idea of considering abstract simplicial complexes, Vishal and I considered more complicated structures that could arise.
If A, B and C are non-trivial mutual friends (i.e. {A, B}, {B, C} and {C, A} belong to the hypergraph, but {A, B, C} does not), then we can describe them as being either unique non-trivial mutual friends (UNTMFs) or non-unique non-trivial mutual friends (NUNTMFs). A set of three NTMFs are described as unique if there is no person D such that {A, D}, {B, D} and {C, D} belong to the hypergraph. Our first example was a set of three UNMTFs, as no-one else knows Vishal, James and their mutual friend.
Non-unique non-trivial mutual friends
An example of non-unique non-trivial mutual friends includes me, Vishal, Jovan and Katya. The simplical complex corresponding to our acquaintancy is given below:
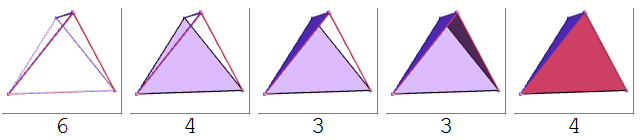
As with all NUNTMFs, the situation is represented by a hollow tetrahedron with between zero and four faces (a solid tetrahedron would correspond to a set of four trivial mutual friends). The possibilities are shown below:
Below each of these simplicial complexes is a number called the encounter count. This is the minimum number of encounters necessary for this relationship to be satisfied, i.e. the number of maximal elements in the partially ordered set of simplices under inclusion. Trivial mutual friends have an encounter count of 1.
Counter-unique configurations
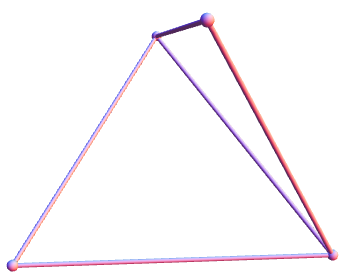
The extremal cases of either zero or four triplets of TMFs in a set of four NUNTMFs are very symmetrical, so Vishal decided upon a new name. Rather than describing the configurations as the tongue-twisting ‘encounter–count–extremal non-unique’, he decided upon the much more manageable ‘counter-unique’. I don’t know of any real-life examples of counter-unique NTMFs, although I have been in a partial tetrahedron where five of the edges and none of the faces were established:
The way in which this peculiar object formed was quite surprising. Radley and I knew each other ab initio, as did Suzy and Miranda. Slightly later, but still ages ago, Suzy met me (thus creating a path graph on four vertices). Radley subsequently met Miranda at their college (Homerton), thus completing a 4-cycle. The fifth edge was completed when Radley met Suzy at the Cambridge Union Society, and we were tantalisingly close to becoming counter-unique non-trivial mutual friends. However, when three of us went to a formal (evening dinner) at Trinity, a face was created and thus the opportunity destroyed.
If you’ve been affected by any of the issues in this blog post, please mention so in the ‘comments’ section below. I would particularly like to hear if you know any real-life examples of counter-unique non-trivial mutual friends, and ideally how they became established.


Non-trivial mutual friends are easy to think of – perhaps the most interesting one I can think of is:
Andrew Carlotti Stephen Pearson Robin Battacharyya Andrew Carlotti
I think I have come up with two possible sets of counter-unique non-trivial mutual friends. The first one, consisting of six pairs, has two unconfirmed links, one meeting still in the future and some information I am not currently allowed to tell you (sorry).
The other consists of four triples. The members are:
1. Andrew Carlotti
2. Sam Cappleman-Lynes
3. Adam Goucher
4. James Rickards
1, 2 and 3 have met at several maths, 1, 2 and 4 met at IMO 2012, 1, 3 and 4 met at IMO 2011 and 2, 3 and 4 have built a snowman together at Trinity.
The unconfirmed one is now confirmed as not an example.
Also, I’ve just noticed that my angular brackets above appear to have been interpreted as formatting. The first example should read:
Andrew Carlotti -(Uncle)- Stephen Pearson -(something to do with quizzing)- Robin Bhattacharyya -(RMM + other maths stuff)- Andrew Carlotti
All the other examples I have so far thought of are either three people who live locally or three people related through maths. In this case the three links are completely unrelated.
Okay, I like your second example of counter-unique NTMFs, and am intrigued to see the first example. Also, I have complete knowledge of the information you’re not allowed to reveal to me.
Really? Perhaps you could tell me what it is then (perhaps on Facebook). I’d be surprised if you do know it.
I think I may have an example for 6 pairs, though I certainly can’t guarantee its correctness:
Graham White and Ceri Fiddes may have met at IMO 2006 (as contestant and deputy leader).
Graham White and David Vasak probably met at some Australian training camp.
Ceri Fiddes and David Vasak met at IMO 2010 (as deputy leader and contestant).
Graham White and Paul Russell met at the Pre-IMO camp 2011 (Paul Russell gave a lecture and Graham was deputy leader).
Ceri Fiddes and Paul Russell met at the Trinity camp last year (2012), and probably at other camps too.
David Vasak and Paul Russell have presumably met at Cambridge (they are Facebook friends).
There are a few ways this could go wrong, and it would be very hard to confirm without consulting one or two of them.
I think two examples (if indeed this is one) are enough, so I’ll stop looking at the EGMO participants list, the UK, AUS and CAN participants on the IMO official site and the list of people at Trinity and Hungary last year (these, along with Facebook and my memory, were my main sources).
If your example does turn out to be counter-unique, then well done. James Aaronson prefers more interesting examples, where the edges are for more different reasons (such as my partial tetrahedron, where the five edges were completely different). Sam Cappleman-Lynes provided an example of a five-edge partial tetrahedron which hasn’t yet been ruined by any faces, involving him, someone he met at school called Evie, a person who happened to meet Sam and Evie at *separate* music concerts, and Ed Godfrey (who has met Evie, but not the elusive concert acquaintance whose name is unknown). We just need unknown guy to meet Ed Godfrey in some contrived situation that’s been deliberately engineered.
James, however, remarked that these partial tetrahedra (more accurately known as ‘diamond graphs’) are not too surprising, since they’re just a pair of people with two NTMFs who haven’t met each other.
Vishal remarked how NTMF triples and counter-unique quadruples are special cases of the general idea of a set of n people such that every k-set has met but no (k+1)-set has met (where 1 < k < n, for non-triviality).
I’m afraid I don’t remember which Evie Sam means…
Another “almost” tetrahedron involving me (and possibly a full tetrahedron, I’m not sure) is Me – Hunter Spink – Jordan Millar – Yunwoo Lee. There may be others.
What shape should that give Ed, and what are the circumstances causing it? The only bits I know of are an edge for you and Jordan, and a possible face for Hunter, Jordan and Yunwoo (all three were at IMO 2011, but may not have met together at any stage).
All of the elements of that involving me are correct – all three edges exist and none of the three faces do. (I do not specifically remember meeting Ceri at that particular IMO, but agree that I probably did).
Perfect! The other edges are certain based on the evidence given by Carlotti, so we need only verify that the face {David Vasak, Ceri Fiddes, Paul Russell} does not exist. I’ll go ahead and ask him…
I am now allowed to tell you my idea for where another CUNTMF may be found. My original set of people doesn’t work, but I expect that it may be modifiable so that it does work. It is based around maths stuff, and cipher challenge prize-giving ceremonies.
Graham Niblo (head of maths at Southhampton, and organizer (I think) of the cipher challenge), has met (Florence Salter/Natalie Behague/Vishal Patil) at the prize-giving ceremony last year, and will meet (Daniel Hu/Andrew Carlotti) at the ceremony this year. A fourth person can probably be found who has met him either at a prize-giving ceremony or who knows him through university, and who has met two of the other people above, on separate occasions.
I had been considering the set Graham Niblo, Andrew Carlotti, Florence Salter and Alex (Luke) Betts, but Luke, while invited to the ceremony four years ago, did not actually go, and I didn’t bother to find out whether he had met Florence, or whether he had met us both at the Royal Society this year.
Also, despite having “complete knowledge of the information you’re not allowed to reveal to me”, Adam seems to have in fact known nothing about it.
Florence Salter has almost certainly met Lex Betts at TCC, and not in the presence of Carlotti or Graham Niblo, so I can confirm that this tetrahedron exists. Well done.
Did you not read it properly? The tetrahedron does not exist because neither Luke nor I (as it happens) have met Graham.
Here is a wireframe tetrahedron I can almost confirm, where the edges are quite different. I will use initials:
EA and GG are schoolmates
EA and AW were at a debating competition
AW and AM are schoolmates
AM and GG met in Israel
GG and AW met at a party
I can say with 90% certainty that EA and AM know eachother; although they are not friends on Facebook I know that their set of very close friends have a huge intersection.
With even more certainty I can say that AM, EE and AW do not form a face as EE and AW have only met at a debating competition, but again I am not completely certain.
Everything involving GG is definite for obvious reasons.
That should read EA
That’s much more interesting than Carlotti’s example, as the meetings are for different reasons. Impressive!
I think I’ve just found a good example a good example. All four people live in Kent and are a similar age, but that’s the only thing linking all four. The people are Andrew Carlotti, Billy Severn, Heather Dower and Andrew Lancaster
AC and BS both went to Ripple School for Year 1 to 3.
AC and HD went to Explorer Scouts together.
AC and AL both go to Sir Roger Manwood’s School.
BS and HD both went to both Walmer Science College and Canterbury College.
BS has met many members of a group of friends including AL, but I can’t guarantee that they’ve met.
HD’s boyfriend is AL’s brother.
Right. Those connections seem sufficiently diverse to be deemed interesting.
wow
here are a few examples/quasi-examples. most of them are pretty boring since they involve situations like myself + 2 people from trinity that i’ve seen individually but never together though i can check they’re facebook friends. i’m guessing that is allowed. personally i have a wide but shallow network of acquaintances so it’s not hard to think of some of these. (i would NOT recommend this. a large amount of diluted friendships simply don’t add up.)
all relevant friendships have been confirmed by excessive facebook stalking except in rare cases where it’s obvious
last names have been omitted
(formerly) example uno:
1 myself
2 sophia
3 alex m
4 aneesh
12 trinity
13 sending me weird freaky texts (ok, here’s the context. there’s this guy called alex from corpus in my year who 13 months ago got a hold of my number via aneesh and started sending me these freaky texts. i didn’t know him at the time. i kept replying to his strange texts trying to out-freak him, thinking phone rape, but turns out it wasn’t, he just felt like doing it. we later met and became friends. also all the corpus people sat at the back row in lectures in the cockcroft and secretly stalked everybody, that’s how they knew me beforehand. don’t ask why.)
14, 23 school (different schools obviously)
24 facebook rape, they don’t know each other
34 corpus
(triples 123 and later 134 have since been formed. this was the most clearcut example)
example dos:
1 myself
2 sophia
3 ingram
4 aneesh
12, 13, 23 trinity (i’ve never seen the other two at the same time)
14 school
24 facebook rape
34 cambridge union
example tres:
1 myself
2 horace
3 alex r
4 nick
12, 23, 24 school
13 maybe i think i met him once at school or something but i can’t remember
14 online community and later real life in a graph theory lecture
34 same online community, never real life (in fact they didn’t know each other by real name until i found this out)
(134 not an online triple because 3 left it before i joined)
example cuatro:
1 myself
2 ram
3 greg
4 john
12 birmingham maths 2007
1->3 i followed the directions on alex’s texts and somehow unintentionally ended up in his room. he recognised me, because:
3->1 lecture stalking
14 trinity
23 corpus
24 no idea
34 school
(234 might be a triple. not sure. can’t say)
example cinco:
1 myself
2 francesca
3 joe
4 matt
12 varsity ski trip (we probably met before at school, but forgot each other)
13 school
23 probably school, they were a year apart
14 trinity
24 trinity a year apart i guess
34 no idea but 3 is a pembroke fresher so something cambridge related
example seis:
1 myself
2 alasdair r
3 alasdair p
4 ben
12 he supervised me for vectors and matrices
13, 14, 34 trinity, i’ve never seen the other two at the same time
23 rowing
24 they live next door
quasi-example siete: (not involving myself)
1 charlie
2 you
3 david
4 vishal
12 that time when charlie shouted your name out in front of the whole magpie and stump audience 😛
13 trinity
14 magpie and stump (unless charlie knows that you and vishal know each other, but i might have to check with him.)
23 imo 2011
24 some random maths camp presumably. you tell me
34 now we just need to get david and vishal to meet each other; maybe they already have done? and you can’t be there with him. tell me how this plan goes
to be honest, the two peoples’ examples directly above this post probably beat all of these for elegance, but i feel this is worth sharing anyway
Hmm, it appears that wireframe tetrahedra are more common than I imagined. Hence, it could be possible that there exists a K_5 somewhere. I can’t help but notice that Vishal seems to feature frequently in these tetrahedra, so he might be a good place to begin.
By the way, it has been mentioned that there are ‘boring’ examples of wireframe simplices arising when people on sports teams meet each other in matches.
correction: you and david didn’t meet at imo 2011 (doh) but i’m pretty sure you know him anyway
Anyway, I neglected to mention that I’m now part of a wireframe *disphenoid*, i.e. opposite edges of the wireframe tetrahedron are for similar reasons. Specifically, we have:
VPP — APG: Met at Trinity College, Cambridge
SEE — PB: Met at Downing College, Cambridge
VPP — PB: Attended the same school in Birmingham
SEE — APG: Attended the same maths camp in Birmingham
APG — PB: Charity blind date in a pub in Cambridge
SEE — VPP: Conversed whilst queueing outside a club in Cambridge
None of the faces have been created yet, and they are unlikely to form in the foreseeable future.
Pingback: Pairwise versus overall | Complex Projective 4-Space