This is the second of a projected three-part series of articles, which will ultimately prove the Turing-completeness of three-dimensional chess. In the first article, I described the basic rules of the game. In this article, I shall show how to construct basic logic gates using rooks, kings and pawns. The final article, which demonstrates Turing completeness, requires a fourth piece, namely the knight.
Constraining motion
With thousands of pieces on an infinite board, the game could quite easily become very chaotic. As such, it is necessary to somehow restrict the motion of the pieces to prevent unexpected moves. The simplest pieces to constrain are pawns, since two pawns of opposite colour on the same vertical file (white below black) block each other:
In the diagram above, horizontal planes are separated by commas, in descending order of altitude. In other words, the black pawn is directly above the white pawn. This convention will be used throughout this article.
Using these pawn couples, it is possible to build a more sophisticated cage for trapping two kings of opposite colours. In the configuration below, all of the pieces are eternally trapped.
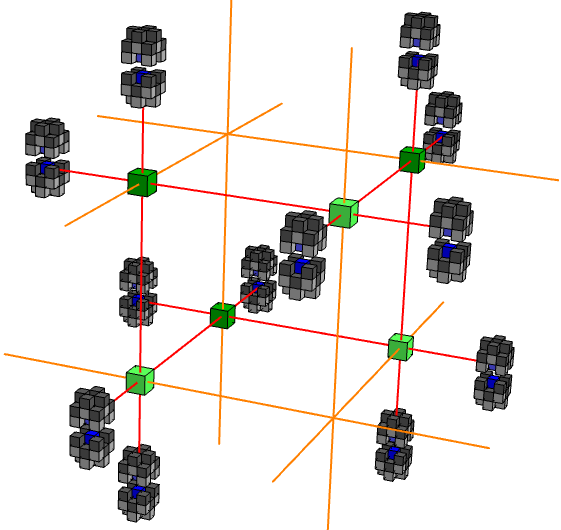
This is not immediately useful on its own, but twelve of them can be used to construct an even more complicated rook cage, where six rooks are trapped in space. If one of the rooks attempts to move, it would result in a king of that colour becoming checked, effecting an immediate loss.
Sorry about drawing the rooks (green) twice as large as the kings (blue) and pawns (grey), but it was necessary to emphasise their comparative importance. The red lines highlight the nonplanar hexagon of mutually pinning rooks. The rooks can protect squares from enemy kings along the yellow lines. We can, in effect, regard the six rooks as two virtual rooks, one of each colour, positioned on the triple intersections of yellow lines. Any excess lines can be blocked by pawn couples.
Corridors, diodes and transistors
Recall that the statement of Turing completeness, in this context, is to be able to devise an algorithm for converting a Turing machine into a chess position, such that white can force a win if and only if the Turing machine halts. Hence, we shall have white ‘in control’ of the game, able to move kings along corridors formed by solid walls of pawn couples. Shown below is an example of a bend in such a corridor:
These are to be used as ‘wires’ to connect components such as diodes and transistors to form more complicated logic gates, latches and switches. We can also construct wires in the vertical plane using exactly the same principle, allowing wires to be crossed without any of those silly conglomerations of three XOR gates.
Shown above is a combined transistor/diode. In ‘diode’ operation, a white king at the bottom left can force his way to the bottom right, but the black rook can prevent reverse flow. In ‘transistor’ operation, a white king can only pass through the upper channel if another white king occupies a position in the bottom channel to threaten the rook.
Important: The black rook is constrained by a rook cage (not shown) to remain on a single vertical file.
By combining these components, it is possible to build latches, switches and logic gates. This is sufficient to prove that three-dimensional chess can emulate any linear-bounded automaton (i.e. a Turing machine with bounded tape).
If we were allowed infinitely many pieces, this would also suffice for Turing-completeness. However, we are not. When restricted to finitely many pieces, it is necessary to be able to store an unbounded amount of information with only finite support. This will be accomplished in the third article, where we implement a register for a counter machine.
Choice gates and alternating Turing machines
We can create two other components, namely white and black choice gates. A white choice gate is simply a T-junction with diodes, which enables a white king to make a choice between either of two exits:
A slight modification of this is to allow a black king to force the choice by being able to guard the two exits. This called a black choice gate, since the black king has control of which exit the white king takes.
When we add these two components, the Turing machine is then upgraded to an alternating Turing machine. Before, we were able to encode PSPACE-complete problems as positions on bounded grids in three-dimensional chess. Now, we can instead encode APSPACE-complete problems. Chandra, Kozen and Stockmeyer demonstrated that this is equivalent to being EXPTIME-complete.

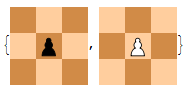



Very interesting. Those rows of little chessboards surrounded by curly braces look just like something one might find in a Mathematica notebook. Are you using Mathematica for your diagrams, and if so are you using a publicly available package to handle the chess diagrams?
Yes, I am indeed using Mathematica. I extracted the chess pieces from screenshots of Wikipedia, then wrote a Mathematica function to convert a three-dimensional array of integers into a list of chessboards, automatically taking the parity of the squares into account.
Pingback: 3D chess is Turing-complete | Complex Projective 4-Space
Pingback: Interesting Esoterica Summation, volume 7 | The Aperiodical
I think I’m missing something – in diode white king moves in fourth plane, but it can’t enter fifth column, because black pawns in plane above would attack him otherwise. So king can’t traverse through this corridor.
Oops, that’s an error. Nevertheless, it can be easily remedied: remove the entire column containing that black pawn, and use a virtual black rook to prevent the white king from entering the column.
Can you make 3D renders of more gates (w/ cutting planes to expose the internals)