Professor Sir Timothy Gowers FRS wrote about the usefulness of a particular proof strategy, known as ‘just do it’. He gives six example problems, providing proofs using this technique. I’ll now give alternative proofs, which use explicit constructions to avoid this idea completely.
Problem 1: Dense set in general linear position
The first problem is to find a dense subset of the plane, where no three points are collinear. We take z = (π + exp(π) i)/24, and let S be the set of all finite sums of distinct integral (both positive and negative) powers of z. For instance, S contains z^8 + z^79 and 1/z, but not 3z^3 or −z^2.
S contains no three collinear points, as otherwise we would have an algebraic relation between π and exp(π). Specifically, if a, b and c are collinear, consider a − b and a − c, where a has largest (or equal-largest) degree when viewed as a polynomial in z. They must be real scalar multiples of each other, i.e. Im((a − b)(a* − c*)) = 0. By the algebraic independence of z and z*, this means that (a − b)(a* − c*) must be a symmetric polynomial in z and z*. Considering the term of leading degree, a must have strictly higher degree (say, n) than both b and c. Now considering the terms divisible by either z^n or (z*)^n, we can deduce that b = c, so they are the same point.
S is dense, as we can easily show (by induction, or whatever) that every sufficiently large disc contains a point of S, and S is self-similar by definition. So we are done.
Problem 2: AP-free colouring of the integers
Is it possible to colour the positive integers with two colours, such that no arithmetic progression is either entirely red or entirely blue? Yes, we can. For example, colour the integer n according to the parity of the integer part of . For each colour, we get arbitrarily thick ‘bands’ that must contain terms of any given arithmetic progression.
Wow, that was really trivial. Much less involved than enumerating arithmetic progressions. If we replaced ‘arithmetic progression’ with ‘infinite recursively-enumerable set’, then the ‘just do it’ method is arguably better.
Problem 3: Packing spheres on the Boolean lattice
This asks for a collection of exponentially many subsets of {1, 2, 3, …, N}, such that the symmetric difference between any two elements of the collection is at least N/3. For N = 24, the binary Golay code is a beautiful example: there are 2^(N/2) = 4096 codewords, and the symmetric difference of any two of them has size 8, 12, 16 or 24.
A generalisation to arbitrary lengths is the notion of a lexicographic code, or lexicode. To construct a lexicode for this problem, we choose the lexicographically least subset of {1, 2, 3, …, N} which differs from existing subsets in at least N/3 positions, and continue until we cannot find any further subsets with this property. This construction necessarily works for the same reasons as Gowers’ ‘just do it’ approach. Lexicodes are also (entirely non-obviously) linear, which means that the symmetric difference of any two sets in the collection is also in the collection.
Problem 4: Finding a transcendental number
Liouville demonstrated that the number 0.11000100000000000000000100…, whose decimal representation is the indicator function of the set {1, 2, 6, 24, 120, …}, is transcendental. Naturally, the proof is a reductio ad absurdum, supposing that there’s a polynomial that vanishes at Liouville’s number.
Problem 5: Infinite matrix whose rows tend to 0, but whose columns tend to 1
This is really trivial. Merely extend the following matrix in the obvious way:
Problem 6: Every distance occurs once
The final of Tim Gowers’ questions is this: “Does there exist a subset Z of the plane such that for every positive real r, there is precisely one pair of points such that
?” He provides a non-constructive proof using transfinite induction up to the initial ordinal with the cardinality of the reals. I’ll leave the ‘don’t do it’ proof as an exercise to the reader…



A few remarks.
I agree that in most cases where there is a just-do-it proof there are also proofs that work by direct construction. However, the just-do-it approach has the advantage of conveying in a more transparent way the fact that the reason the example exists is that there are not too many constraints. With a direct construction, one has no feel for whether it works because of some kind of miracle or whether it is just one of many different constructions that would do the job. Also, sometimes a direct construction is basically just an explicit implementation of the just-do-it approach, so isn’t really an alternative proof.
Turning to your proofs, a fully detailed version of your first proof would be much more complicated than the just-do-it approach, since it would require showing the algebraic independence of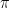 and
and 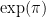 (though an indirect argument could be used to find two non-explicit algebraically independent numbers — but presumably you wouldn’t like that). And even given those numbers, it is hard to tell whether the proof works by magic or whether it is very flexible.
(though an indirect argument could be used to find two non-explicit algebraically independent numbers — but presumably you wouldn’t like that). And even given those numbers, it is hard to tell whether the proof works by magic or whether it is very flexible.
For Problem 2, I don’t understand your proof that the set doesn’t contain arbitrarily long APs, though I agree that the result is true. But if you make the lengths of the intervals grow like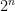 then proving that the example works is indeed very simple. An advantage of the just-do-it approach in this case is that the argument generalizes to a vast number of other situations: essentially any infinite Ramsey problem where the size of the object you are colouring is at least the size of the number of objects you have to colour. So the just-do-it proof gives you more insight than a specific construction like one based on intervals of increasing length.
then proving that the example works is indeed very simple. An advantage of the just-do-it approach in this case is that the argument generalizes to a vast number of other situations: essentially any infinite Ramsey problem where the size of the object you are colouring is at least the size of the number of objects you have to colour. So the just-do-it proof gives you more insight than a specific construction like one based on intervals of increasing length.
For Problem 3, the Golay code (or anything similar) is another example where you miss out on the insight that the existence of such a set is in some sense “obvious”. As for the lexicodes, that I would call just an implementation of the just-do-it approach and not something significantly different.
For Problem 4, again Liouville’s construction doesn’t give you the understanding that transcendental numbers aren’t special kinds of things that need careful construction.
The example you propose for Problem 5 is precisely the same as the example that comes out of the just-do-it approach. So the only difference here is that you produce the example out of thin air and the just-do-it approach shows how you can discover it for yourself.
Problem 6: I’ll have to think about that exercise. The problem is trivial if you use the just-do-it approach. Even if the construction I’m missing is an easy one, the fact remains that I have to think to find it, whereas I don’t have to think to use the just-do-it approach.
Added a few moments later: I now understand your argument about the APs, and withdraw my small remark about needing the widths of the bands to grow faster. However, the point about generalizability remains.
Agreed.
I personally don’t really like Gowers’ proof of 6th problem. It is nice and shows how transfinite induction can be used in non-obvious way, but it uses AC. For me, axiom of choice and its relatives are intuitivelly true, but after all this proof cannot be embedded in axioms of ZF set theory. Does your don’t-do-it proof (if you have one) use axiom of choice?
I don’t have a don’t-do-it proof for the 6th problem, and it is generally in cases such as this (where we have to deal with uncountably many constraints) that the combination of just-do-it and transfinite induction are actually unavoidable. For example, proving that there exists an infinite game where neither player has a winning strategy requires the Axiom of Choice, since ZF is consistent with no game having this property. Although I solved that particular one using a just-do-it approach (systematically destroying every possible strategy), there are apparently more explicit constructions (still requiring choice).
Pingback: Ring of periods | Complex Projective 4-Space