One of the more familiar examples of fractal curves is the Koch snowflake. It is a closed curve of infinite length and Hausdorff dimension log(4)/log(3), homeomorphic to the unit circle. It bounds a region which, when combined in two different sizes, can tile the plane (as noted by Benoit Mandelbrot):
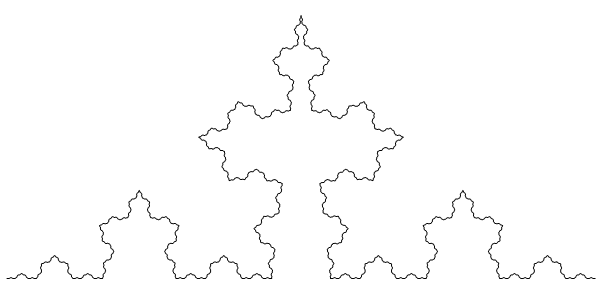
The Koch snowflake can be constructed from three copies of the von Koch curve. This is a self-similar fractal curve, composed of four copies of itself, each scaled by . Varying the value of σ between ¼ and ½ yields a family of fractal curves, with Hausdorff dimension ranging from 1 (a straight line) to 2 (a spacefilling curve):
In each of the curves, the same value of σ is used for all iterations. If, instead, we vary the value of σ, then the Hausdorff dimension is a function of the limiting value of σ (assuming the limit exists). In the following curve, σ successively takes on the values {1/4 + 1/5, 1/4 + 1/6, … , 1/4 + 1/n, …}, so the limiting value of σ is ¼, and the Hausdorff dimension is 1. Hence, this is not technically a fractal. However, an easy computation will verify that the length (product, over all iterations, of 4σ) is infinite.
In other words, we have a non-fractal curve that nevertheless exhibits many of the same properties as fractal curves (infinite length, approximate self-similarity, etc.). On the other hand, if the values of σ converge to ¼ sufficiently quickly, then we obtain a curve of finite length.




How is “sufficiently quickly” defined? If the quasi fractal case has sigma = 1/4 + 1/n, does the non-fractal case have sigma = 1/4 + 1/n^2 or some other power of n? If so, where is the threshold power of n between curves of finite and infinite length?
Infinite length occurs if and only if the infinite product of (4 sigma) diverges, which occurs if and only if the infinite sum of (sigma – 1/4) diverges. Hence, your sigma = 1/4 + 1/n^2 has finite length, as does the curve obtained be replacing 2 with any other power greater than 1.