Supercoiling

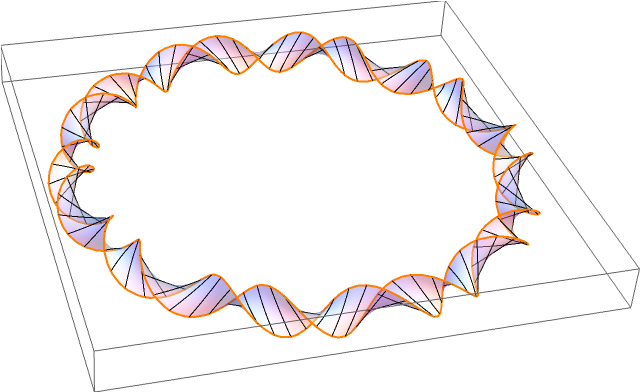
Quite a while ago in the Eagle pub in Cambridge, James Watson and Francis Crick announced the double-helix structure of DNA. This discovery was based on earlier X-ray diffraction experiments by Rosalind Franklin. In eukaryotic organisms such as ourselves, DNA has a linear structure (admittedly tightly coiled into a chromosome, but there is no difference from a topological perspective). By comparison, bacteria have a circular loop of DNA:

In the diagram, an orientable surface (Seifert surface) is drawn, making the DNA into a ribbon. It is not immediately obvious that the surface must be orientable, without considering DNA at a more atomic level. Specifically, why can’t DNA form the boundary of a Möbius strip?

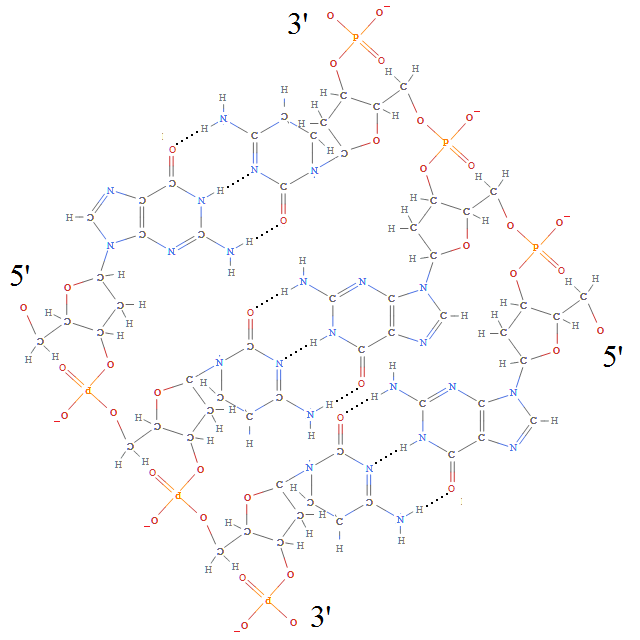
Each of the deoxyribose-phosphate backbones is directed, possessing a 3′ and 5′ end (pronounced ‘3-prime’ and ‘5-prime’, respectively, which is nice because both 3 and 5 are primes). And, as you can see, the opposite sides of the double-helix are directed in opposite directions, so the number of twists must be a full integer, rather than the half integer necessary for a Möbius band.

Now, if we forget the base pairs connecting the two deoxyribose-phosphate backbones, we obtain two linked (topological) circles. The unique topological invariant specifying how two closed curves (able to pass through themselves but not each other) are linked is the linking number. To prove this fact, we homeomorphise space so that one of the unknots is a fixed circle, and then observe that the complement of this circle has fundamental group .

Given a three-dimensional parametrisation of the unknots, the linking number can be computed by Gauss’s linking integral:

In particular, this determines the signed area of the image of the Gauss map, which is a multiple cover of the sphere.

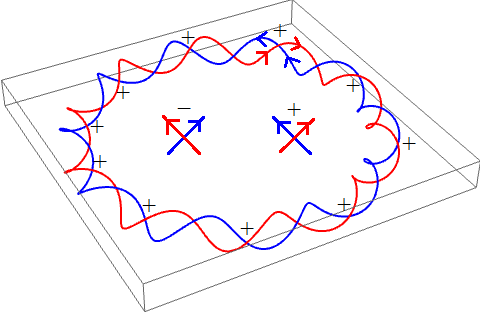
Alternatively, we can draw a diagram of the directed curves and count signed crossings where the red curve passes over the blue curve:

Consequently, the linking number of this DNA strand is +10.

There is an enzyme called topoisomerase which changes the linking number of DNA without any net effect to the local topology of the DNA. (That is to say, the labelled graph formed by associating a vertex to each atom and edge to each bond is unchanged.) Indeed, there are several different types of topoisomerase, which increment or decrement the linking number by different amounts.

Now suppose we take the entire DNA loop and bend it into a lemniscate (this is a homotopy, thus invisible to topologists). The linking number must remain constant, but we have added what is known as a writhe. This results in a corresponding change to the number of twists in the DNA double helix, by the formula (the linking number is the signed sum of the writhes and twists).

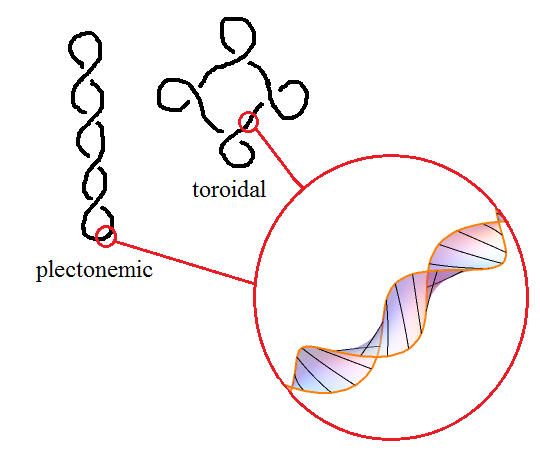
Now, DNA minimises its energy when there is precisely one twist per 10.4 base pairs. Hence, if the linking number is different from this, the DNA will automatically introduce writhes to compensate in a process known as supercoiling. When the writhe number is significant, DNA takes on a superhelical structure. Two common structures that occur in this way are the toroidal and plectonemic structures:

You can observe supercoiling with a plain piece of string. If you keep twisting it, then eventually the strain will be too much and it will supercoil into a larger helix. Eventually, after further twisting, that helix will super-supercoil into an even larger helix, and — if the string is sufficiently long, such as a metre-long string with one end held fixed and the other attached to an electric motor — you can obtain multiple nested levels of supercoiling in this manner. Indeed, this phenomenon occurs in chromosomes, with extra structural scaffolding (known as histones) to bind it in this tight efficient structure: a human cell nucleus is only 5 microns wide, but contains nearly a gigabyte of genetic material.