I overheard mention of a particular problem on a recent British Mathematical Olympiad, namely the following:
A number written in base 10 is a string of 3^2013 digit 3s. No other digit appears. Find the highest power of 3 which divides this number.
Personally, I bemoan such problems that are trivialised by the knowledge of advanced theorems, as it enables competitors to gain an unfair advantage by rote-learning many results rather than demonstrating creative mathematical thought. In this case, the question is trivialised by a rather elegant but little-known lemma called lifting the exponent.
So, what does the lemma state? Firstly, we establish the following definition:
Definition: the p-adic valuation v_p(n) of an integer n to be the highest power of p which divides n. For example, v_2(40) = 3, since 2^3 divides 40 but 2^4 does not.
Then the lemma is as follows:
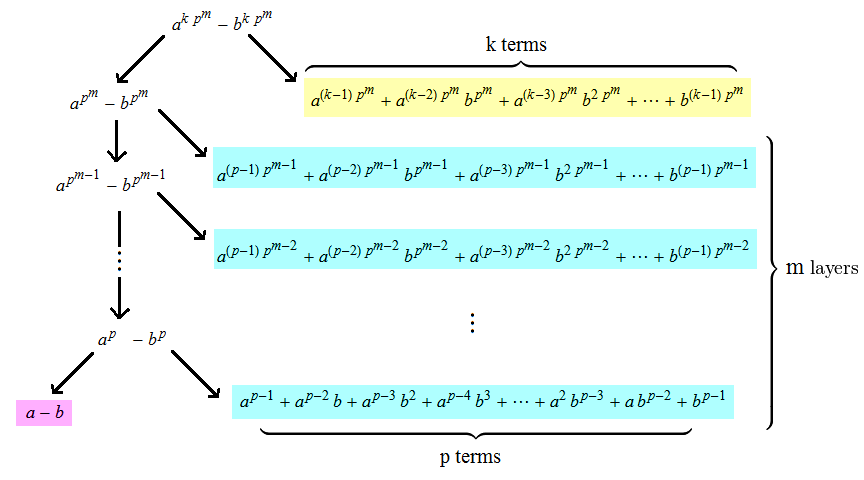
Theorem (lifting the exponent): Let p be an odd prime, and a and b integers such that neither a nor b is divisible by p, but p divides their difference a − b. Then v_p(a^n − b^n) = v_p(a − b) + v_p(n).
Why is this true? The idea is that we factorise a^n − b^n like so, where n = k p^m and k is not divisible by p:
The factors in the final factorisation are highlighted. It is clear that it is sufficient to prove that the yellow factor is coprime to p (which is easy, since all of the terms are congruent modulo p and are non-zero) and each of the blue factors are divisible by p (easy for the same reason) but not by p², as we shall prove:
-
If a and b are congruent modulo p², this is again trivial for the same reason as before.
- Otherwise, we have to actually rely on the property that p is odd (if p = 2, we need a and b to be congruent modulo 4 rather than modulo 2). We let x and y be equal to a^p^i and b^p^i, respectively, for the obvious value of i, such that the factor is of the form:
Γ = x^(p-1) + x^(p-2) y + x^(p-3) y^2 + … + y^(p-1)
Then we set y = x + lp for some integer l (which we can do, since y and x are clearly congruent modulo p). Expand the factor Γ to produce a sum of binomial expansions; we can ignore all terms of order p² and higher since we’re only interested in the residue modulo p². This gives the following expression:
The rightmost term vanishes, leaving something that is clearly not divisible by p². Consequently, the proof is complete and the result follows immediately.
Zsigmondy’s theorem
Another useful fact concerning a^n − b^n is this: except in a few exceptional cases, it has a new prime factor p that does not occur in any of a − b, a² − b², a³ − b³, …, a^(n−1) − b^(n−1). The exceptions to the rule are the following:
-
a = 2, b = 1, n = 6: we have 2^6 − 1^6 = 63, whose prime factors are 3 and 7, which occur in 2^2 − 1^2 and 2^3 − 1^3, respectively.
- a + b is a power of 2, and n = 2: then a² − b² = (a + b)(a − b). The first factor is a power of 2 (so no new primes there), and the second factor is itself the previous term in the sequence (so, by definition, no new primes there either).
A related statement about Fibonacci numbers (where the integers a and b are replaced with irrational algebraic integers, and an extra factor of √5 slips in) is known as Carmichael’s theorem. Zsigmondy’s theorem and Carmichael’s theorem can be mutually generalised to other Lucas sequences.