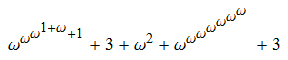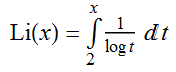This is the first of a projected two-part series of articles about fast-growing functions.
The first part (‘fast-growing functions’) will introduce the concept of a fast-growing hierarchy of functions, use some notation for representing large numbers, make an IMO shortlist problem infinitely more difficult, and solve it by the well-ordering of the ordinal ε_0.
The second part (‘really fast-growing functions’) will describe Harvey Friedman’s n and TREE functions in detail, before exploring models of computation such as Turing machines and lambda calculus to reach and surpass the Busy Beaver function Σ.
Fast-growing hierarchy
We’ll define a sequence of increasingly fast-growing functions. For a relatively slow start, let’s begin with the function f_1(n) = n+2. Applying f_1 to the natural numbers gives the sequence {3, 4, 5, 6, 7, 8, …}.
Now, we use something called recursion to speed things up somewhat. For each positive integer α, we define f_(α+1)(n) = f_α(f_α(f_α(… f_α(2)…))), where there are n−1 copies of f_α. To avoid the ellipses, we can represent this as the recurrence f_(α+1)(n+1) = f_α(f_(α+1)(n)) with initial condition f_α(1) = 2.
So, f_2(n) = 2n and f_3(n) = 2^n. We’ve very quickly moved from addition via multiplication to exponentiation, so it is clear that later terms will be quite fast indeed. The fourth function gives a tower 2^2^2^2^ … ^2 (evaluated from right to left) of n twos. Using Knuth’s up-arrow notation, this is written as 2↑↑n.
Most weak upper bounds encountered in elementary Ramsey theory (chapter 3 of MODA), such as Ramsey’s theorem and van der Waerden’s theorem, correspond to functions early on in this hierarchy (the naïve bound for van der Waerden is roughly f_4, if I remember correctly).
The largest complete graph which can be three-coloured without a monochromatic triangle, an object in Ramsey theory
We also get functions in Ramsey theory which grow more quickly than any of these functions. In the second part (really fast-growing functions), I’ll describe Friedman’s functions n and TREE, the latter being much faster than anything described in this first part.
Coins in boxes
A recent question on the International Mathematical Olympiad involves a sequence of six boxes, each of which initially contain one coin.
There are two different operations you’re allowed to do:
- Remove a coin from box i and add two coins to box i + 1.
- Remove a coin from box i and swap the contents of boxes i + 1 and i + 2.
The question asks whether it’s possible to get 2012^(2012^2012) (or, in Knuth’s up-arrow notation, 2012↑↑3) coins in the final box. This may seem daunting at first, but it’s not too difficult. Iterating operation 1 allows you to get from (a, 0) to (0, 2a) quite easily. You can get from (a, 0, 0) to (a-1, 2, 0), then (a-1, 0, 4). Applying operation 2, the next step is (a-2, 4, 0), then (a-2, 0, 8), and so on. Recursively, we can get to (0, 2^a, 0).
With more boxes, we can go even further, and get from (a, 0, 0, 0) to (0, 2↑↑a, 0, 0). This pattern generalises in the obvious way.
It transpires that we can indeed get 2012↑↑3 coins in the sixth box. James Cranch asked Maria Holdcroft how many boxes are required to get 2012↑↑(2012↑↑3) coins in the final box, expecting the answer to be seven. She demonstrated that, surprisingly, it’s possible with merely six boxes. Try it yourself!
The Ackermann function
We’ve defined functions f_α for all positive integers α. Can we find a function which eventually overtakes all of them? Indeed, we can; let f_ω(n) = f_n(n). This creates the ‘diagonal’ sequence {3, 4, 8, 65536, 2↑↑↑5, 2↑↑↑↑6, …}. We’ll call this the Ackermann function, although different authors use different definitions. For instance, the Ackermann function could be defined as the maximum number of coins you can get from an initial configuration of n boxes each containing one coin, and it would have a very similar growth rate to every other definition of the Ackermann function.
By the way, ω is the first ordinal greater than all integers. Ordinals are a type of infinity, which I mentioned briefly when discussing combinatorial game theory. I mentioned them again in connection with fusible numbers, and they’re even more important here. You can consider ω to be the limit of the sequence 1, 2, 3, 4, 5, … of natural numbers. The first few ordinals are {1, 2, 3, 4, …, ω, ω+1, ω+2, …, 2ω, 2ω+1, …, 3ω, …, 4ω, …, ω^2, …}, where the ellipses indicate omission of infinitely many terms! We’ll use ordinals as subscripts for this fast-growing hierarchy of functions.
By recursion on f_ω, we can define a new function f_(ω+1). The first few terms are {2, 4, 65536, 2↑↑↑↑…↑↑↑↑65536}, where there are 65534 up-arrows in the fourth term. The largest number used in a serious mathematical proof, Graham’s number, is roughly the 67th term in this sequence produced by f_(ω+1). It is the upper bound for a particular question in Ramsey theory (the corresponding lower bound is 12).
Proceeding in this manner, we can recurse to get f_(ω+2), f_(ω+3), …, and then diagonalise to get f_(2ω). Technically, this should be written f_(ω.2), since ordinal multiplication is not commutative, but notational abuse is common in the world of ordinals. Repeating this process, we get f_(ω.3), f_(ω.4), et cetera, and we can diagonalise to get f_(ω^2). It’s not too hard to see that all ‘polynomials’ (ordinals below ω^ω) can be obtained in this way. Finally, another diagonalisation gives us f_(ω^ω).
Going further, you can get ω^ω^ω, ω^ω^ω^ω and so on. The supremum of these (writing this as ω↑↑↑2 is a gross abuse of notation which will enrage most pure mathematicians) is called ε_0, and is the smallest fixed point of n → ω^n. We’ll get to this later.
Like a C8
Every year, lots of problems are submitted for inclusion in the International Mathematical Olympiad. The reasonably good ones get onto a shortlist, of which six are cherry-picked for the test itself. There are some gems on the shortlist which are neglected, such as this particular question from Austria (classified as C8, i.e. the hardest combinatorics problem on the shortlist in 2009):
For any integer n ≥ 2, we compute the integer h(n) by applying the following procedure to its decimal representation. Let r be the rightmost digit of n.
-
If r = 0, we define h(n) = n/10, i.e. we remove the final trailing zero.
-
Otherwise, if r is non-zero, we split the decimal representation of n into a maximal right part R that consists solely of digits not less than r. The remaining left part is called L (either empty or terminates in a digit less than r). We then define h(n) by concatenating L followed by 2 copies of R−1. For instance, with the number n = 17151345543, we get L = 17151, R = 345543, and h(n) = 17151345542345542.
Prove that, for an arbitrary integer n ≥ 2, repeated application of h eventually reaches 1 in a finite number of steps.
For example, we get 2 → 11 → 1010 → 101 → 1000 → 100 → 10 → 1.
This is non-trivial (hence its rating as C8). Still, we can improve it to make it so much harder! Instead of appending 2 copies of R−1, we append c copies, where c initially begins at 2 and increments every time we apply this process. So, the second time, we append 3 copies of R−1, and so on. This time, starting with n = 2 gives us a longer progression:
2 → 11 → 101010 → 10101 → 10100000 → 1010000 → 101000 → 10100 → 1010 → 101 → 1000000 → 100000 → 10000 → 1000 → 100 → 10 → 1.
Even though C8 was phrased in that way, it’s silly to think of the ‘numbers’ as integers rather than strings of decimal digits. Indeed, the restriction to decimal is arbitrary and unnecessary, and we should instead think of them as sequences of positive integers (the fourth term in the above process is {1,0,1,0,1} rather than the number 10101). Still, we’ll write them without commas for brevity.
Let’s invent a function g which maps strings to ordinals. We’ll map the string “0” to the ordinal g(“0”) = 1. If we have something like “3420001107000”, we’ll map the string to the ordinal ω^g(“231”) + 1 + 1 + 1 + ω^g(“00”) + 1 + ω^g(“6”) + 1 + 1 + 1. Specifically, we separate it into substrings of non-zero digits, decrement the digits in them, map them to ordinals, raise ω to the power of those ordinals, and add them all together. Applying this recursively, our string “3420001107000” is mapped to this ordinal:
Removing a terminal zero in a string reduces the corresponding ordinal by 1. Applying the other operation causes ω^n to be replaced with (ω^(n−1)).c, where c was defined in the question. This also results in the ordinal decreasing, since c < ω. In other words, are long process has an associated sequence of strictly decreasing ordinals.
Since the ordinals below ε_0 (and indeed all ordinals) are well-ordered, there is no infinite decreasing sequence of them. Hence, this sequence must terminate and reach 1 in a finite amount of time. QED.
It does, however, take a very long amount of time for the process to terminate. If we begin with a single digit n (remember, we’re not restricting ourselves to decimal, so n can be as large as we like), we can define a new function T(n) which gives the number of steps it takes for the process to terminate. For instance, T(1) = 0, T(2) = 16 and T(3) is large. To give an idea as to the size of T(3), the first few strings in the sequence beginning with “3” are:
3 → 22 → 212121 → 212120212120212120212120 → 21212021212021212021212 → 212120212120212120212111111 → 212120212120212120212111110212111110212111110212111110212111110212111110 → …
This function T grows at roughly the same rate as the function f_(ε_0) in our fast-growing hierarchy (by comparison, the original problem C8 only gives a pathetic growth rate around f_4). A very similar function (see Goodstein’s theorem) exceeds Graham’s number for n = 12. It wouldn’t surprise me if the same applies to our function T(n).
Goodstein’s theorem (and probably our modified question C8′) cannot be proved in Peano arithmetic (basic operations together with basic logic and finite induction). This is why C8′ is so much harder than C8, and consequently far too difficult to appear on an IMO. As far as I know, all IMO combinatorics problems can be proved in Peano arithmetic.