Complex Projective 4-Space

The ordinary Cantor set is obtained by removing the middle third of a unit line segment and iterating. The resulting set of points is uncountable, nowhere dense and has zero measure.

It transpires that the construction can be modified to give a set with non-zero measure, the so-called fat Cantor set. Note that in the previous construction, we remove intervals whose total length sums to 1 (namely 1/3 + 2/9 + 4/27 + 8/81 + …). If, instead, we remove smaller intervals so that the sum converges to a value below 1, then the set left over will have non-zero measure. An example of this is the Smith-Volterra-Cantor set, with measure 1/2.

Indeed, by a similar construction, we can get nowhere dense sets with measure arbitrarily close to (but not equal to) 1.  This result is so counter-intuitive that the fat Cantor set was proclaimed ‘bizarre mathematical object of the week’ by Ben Elliott et al.

In 2001, Lee Sallows generalised the concept of a magic square, replacing the integers in each cell with subsets of the plane. He calls such a configuration a ‘geomagic square’ if the subsets in every row, column and diagonal can tile the same shape. One of my favourites is this one, where nine distinct hexominoes appear:

One of Lee Sallows’ geomagic squares

He has produced geometric versions of many extant magic squares (including Dürer’s square), as well as some examples which do not have non-trivial numerical analogues (e.g. a 2 by 2 geomagic square).

Every geomagic square gives a numerical magic square (by replacing each shape with its area). Technically, this isn’t quite true in general, as there exist non-measurable subsets of the plane. This difference is even more apparent in three dimensions, where the Banach-Tarski paradox facilitates a generalised ‘geomagic square’ where one line is a proper subset of another! (If you want to learn about the Banach-Tarski paradox, do not watch this video.)

Tsukamoto and Miyazaki of Kyoto University have discovered that three states are sufficient to enable gliders to exist on a Penrose tiling, rather than four. The following video demonstrates their discovery together with a periodic emitter in an augmented rule:

[youtube=http://www.youtube.com/watch?v=6xVLpP25DRQ]

On a related topic, my paper on the original Penrose gliders is now online. The derivation for sequence A215878 is included, which makes heavy use of Lindenmayer systems to describe the fractal paths traced out by the kite-and-dart gliders.

Suppose a Yorkie chocolate bar has a resistance of precisely one ohm. Can you determine the resistance between two vertices of the tetrahedron, which Rychlik is holding in the picture below? (Hint: Use the Y-Δ transform and formulae for resistors in series and parallel.)

Yes, it’s 1/2 ohm. Similar analysis has been performed on the other Platonic solids, with the most complex being the dodecahedron (20 vertices and 30 edges). On a related topic, there was a challenge in the Google Labs Aptitude Test to determine the equivalent resistance between two points separated by a knight’s move on an infinite grid of ideal one-ohm resistors. Some complicated Fourier analysis gives the result as 4/π – 1/2, as does successive approximation followed by use of Robert Munafo’s Rilybot Inverse Equation Solver (a very useful tool for enabling one to dine with a girl whilst keeping her ex-boyfriend safely away by organising an [insert irrational constant]th birthday party for him!).

Squared squares (such as the one above, the logo of the Trinity Mathematical Society) were discovered by considering networks of resistors. Place copper strips along the top and bottom of the square and apply a voltage between them. The resistance is unchanged when horizontal lines are replaced with copper strips and vertical lines are replaced with insulating strips. Then, the resistance across each square (including the large one) is one ohm. Consequently, this squared square corresponds to a network of one-ohm resistors with a total resistance of one ohm:

The same argument applies to squared cylinders. Squared tori, on the other hand, are substantially easier to find: a 5×5 torus can be dissected into two squares of sizes 3×3 and 4×4, where {3,4,5} is a generic Pythagorean triple.

Finally, don’t forget that it’s Cipher Tuesday tomorrow. The cipher will be published at 00:01 UTC. I look forward to seeing you in the solvers’ area.

Let’s consider the group S6 of permutations of {1,2,3,4,5,6}. For fairly boring reasons, we can find S5 living inside there — the subgroup which fixes the element ‘6’. More generally, S(n-1) is contained within Sn.

S6 is special, though, since there’s actually a well-disguised S5 hiding in there, which isn’t obvious at all. One way of proving its existence is actually to find it, by writing down a subgroup consisting of 120 permutations and showing that it’s isomorphic to S5. However, that’s ugly, uninsightful and unworthy of inclusion here. Fortunately, there are more elegant ways to see what’s going on:

The Elliott configuration

The Elliott configuration (above) is a colouring of K6 we explored when finding five-dimensional and four-dimensional Bettsian sets with no symmetry. Indeed, it is not difficult to show that the colouring of the graph above renders it asymmetrical. However, if we allow colours to be permuted, we suddenly acquire a large bunch of symmetries.

Label the vertices A,B,C,D,E,F from top-left clockwise. We can reflect in the vertical axis, i.e. permuting the vertices with (AB)(CF)(DE) in cycle notation, to transpose the colours red and yellow. Similarly, the 5-cycle (ACFED) leaving B fixed causes the five colours to be cycled (blue → green → yellow → red → purple). This is sufficient to show that any permutation of the colours can be obtained by permuting the vertices, and this permutation is uniquely determined (by asymmetry!).

In other words, we have a group isomorphic to S5 (permutations of five objects) sitting inside S6 (permutations of six objects) as a subgroup, but not in the trivial way. An immediate corollary is that we can also find a non-trivial A5 hiding inside A6, which has a couple of other elegant constructions:

Rotations of an icosahedron

Consider the six ‘diameters’ of an icosahedron. Every rotational symmetry causes the diameters to be permuted, so the rotational symmetry group (isomorphic to A5) lies inside S6 in a non-trivial way. These permutations of diameters are actually all even permutations, so we get the stronger result that A5 inhabits A6.

To see that the rotational symmetry group of an icosahedron is indeed A5, consider the centres of each of the triangular faces. They can be partitioned into five sets of four points, with each set describing a regular tetrahedron. The rotational symmetries of the icosahedron correspond to even permutations of the five tetrahedra.

PSL(2,5)

A point on the projective line can essentially be represented as a ratio. Over the finite field F5, there are six such ratios, namely 0/1, 1/1, 2/1, 3/1, 4/1 and 1/0. The group of projective transformations PSL(2,5) permutes these six points and is isomorphic to A5. Again, all permutations obtained in this manner are even permutations, so A5 inhabits A6 in a non-trivial way.

These projective special linear groups are quite awesome. PSL(2,7) is isomorphic to the symmetries of the Fano plane (see the end of the projective geometry chapter of MODA) and the Klein quartic. PSL(2,11) is found as a maximal subgroup in the Mathieu group M11 and as the symmetry group of the 11-cell.

Vladimir Arnold observed how exceptional objects sometimes occur in groups of three, such as PSL(2,5), PSL(2,7) and PSL(2,11). He coined the term Trinity to refer to these families, a word I highly approve of…

Suppose we took a solid unit cube and balanced it on a vertex. Next, we spin the cube really quickly about the vertical axis, producing a solid of revolution:

Clearly, the top and bottom are two identical cones produced by revolving a line segment passing through the axis of rotation. What about the thing between them? It is a quadric surface (three-dimensional conic) called a hyperboloid of one sheet. Alas, this name invariably reminds me of a television commercial for a particular brand of kitchen towels:

[youtube=http://www.youtube.com/watch?v=Xknub_pILt8]

The hyperboloid of one sheet is a doubly ruled surface, meaning that at each point we can find two straight lines drawn on the surface of the hyperboloid which pass through the point*. The only other doubly ruled surfaces are the plane and hyperbolic paraboloid.

* Proof: The hyperboloid is the surface swept out when one of the edges of the cube is revolved about the axis, so must be at least singly ruled. However, the hyperboloid possesses bilateral symmetry, so we can find a second family of lines by reflecting the first family.

One may ask what the volume of the revolved cube is. After some pretty easy stuff involving Pythagoras and vectors, we obtain the various dimensions of the cross-section of the revolved cube:

The two cones each have volume (2 sqrt(3)/27)π, and the hyperboloid has the Cartesian equation 2x²+ 2y² – 4z² = 1, where the centre of the cube is the origin. Basic integration gives a volume of (5 sqrt(3)/27)π for the hyperboloid, so the entire solid has volume π/sqrt(3). It is interesting to note that this total volume, which was obtained in a very piecewise manner, is simpler than the volumes of its conical and hyperbolic components.

As a brief summary, I posted about the three-dimensional generalisation of a particular two-dimensional problem by Alexander Betts. In case you haven’t read it, or didn’t understand it, I’ll explain the ideas again here.

A finite set S of n points in d-dimensional space R^d is Bettsian if, for every point X in S, the set of distances to the remaining n−1 points is the same regardless of the choice of X. Here’s a concrete example in two dimensions, namely the vertices of this rectangle:

The distances from each point to the other three are {3, 4, 5} (the last being the diagonal length), irrespective of which vertex you choose. This example also has the property of being vertex-transitive, i.e. we can rotate and/or reflect the rectangle to move any specified vertex to any other specified vertex whilst preserving the shape. Informally, this means that ‘all vertices are identical’.

All vertex-transitive sets are necessarily Bettsian, but does the converse also hold? In one dimension, it’s pretty trivial to see that the only examples have one or two points (consider the distance between the leftmost and rightmost point). In two dimensions, it’s less easy to see that all Bettsian sets must be vertex-transitive, but again it is true (as a corollary of the original question from the 2011 Romanian Masters of Mathematics competition).

A natural question to ask is whether this holds in all dimensions. After my original post, James Cranch provided a 15-dimensional counter-example. With similar principles, it’s possible to reduce the number of dimensions to six. Ben Elliott and I quickly found this particular example:

We embed this graph K7 into 6-dimensional space, ensuring that the blue edges are length 1 and the red edges are some other length (1.001 should suffice). There is enough ‘room’ for us to be able to prescribe any combination of edge lengths, as long as they are sufficiently close together (imagine a wire tetrahedron in three-dimensional space). It is clear from the graph that this corresponds to a Bettsian set which is not vertex-transitive.

The same proof does not immediately work in five dimensions, since we can’t colour K6 with two colours to result in a Bettsian graph which is not vertex-transitive. Fortunately, using more colours actually works. Three is actually sufficient, as demonstrated by the following graph:

So, letting the green edges be 1.001, the purple edges be 1.002 and the rest be unit length, we have a five-dimensional non-vertex-transitive Bettsian set. This colouring approach fails spectacularly for smaller complete graphs, and we can conclude that the smallest non-vertex-transitive Bettsian sets have at least six vertices.

Much harder in R^4 and R^3

Reducing the number of dimensions then becomes much trickier. The edge lengths are no longer reasonably independent, so we can’t just choose values arbitrarily. We want to have as much freedom as possible, so we’ll give the previous graph five colours instead of three:

If we set blue edges to have length 20, green edges to have length 18, yellow edges to have length 16, red edges to have length 14, and purple edges to have length 12.6815188243… (actually the root of a horrible polynomial involving an unsolvable quintic!), then the entire thing collapses down into four dimensions. Moreover, this is actually consistent, as we don’t break any triangle inequalities, tetrahedral inequalities etc. More than being merely vertex-intransitive, we have no symmetries whatsoever!

This problem is so hard in three dimensions that we haven’t solved it*. This tends to be a common theme in mathematics: two and fewer dimensions are too trivial, whereas high dimensions enable crazy constructions. It seems to be the case that three dimensions is always the last case to be solved (c.f. Poincare conjecture), with R^4 not far behind.

* We found that up to similarity we have precisely one degree of freedom for the 5-colour K6. There is also a one-parameter family of vertex-transitive solutions of this form, where three colours are identical and the shape is a twisted prism. Regular octahedra mark ‘crossroads’ where these one-parameter families of twisted prisms meet. It’s entirely possible that, just like R^2, all Bettsian sets in R^3 are vertex-transitive. If so, we can fully characterise them.

If you take an object and rotate it by 360° about a particular axis, it will return to its original orientation. Certainly, every object you’re likely to have seen obeys this basic principal. If you’re naive, you may actually believe that this applies to everything — an understandable mistake.

Consider this perfectly innocent-looking Möbius strip. I’m going to assume without loss of generality that you understand the properties of Möbius strips. You’ll know, therefore, that it only has one side of ‘length’ 720°, as opposed to two sides of length 360°.

As well as being the double-cover of SO(2), spin(2) is isomorphic to SO(2) (the rotations of a circle). This means I can tear along the lateral line of the Möbius strip to turn it into an ordinary band. It’s also isomorphic to U(1), the group of complex numbers of unit modulus.

SO(3) and Spin(3)

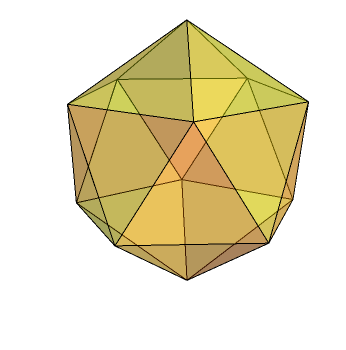
Things become more interesting in three dimensions. We have SO(3), which are the familiar rotations of a sphere. It has three interesting finite subgroups, namely the rotations of an icosahedron, the rotations of a cube and the rotations of a tetrahedron. Any other finite subgroup of SO(3) is boring.

We can describe a rotation by a vector (x,y,z) on its axis and a magnitude w = 2 arccos(θ), where θ is the angle of rotation. Scaling the vector such that w² + x² + y² + z² = 1, we obtain a mapping between the rotation and a quaternion w + xi + yj + zk. It is of great importance that this is a homomorphism from the group of unit quaternions to the group of rotations.

Note that the quaternions q and −q represent the same rotation. In other words, the group of quaternions is isomorphic to the double cover Spin(3) of the rotation group SO(3). The ‘interesting’ subgroups of SO(3) correspond to interesting subgroups of Spin(3):

• The binary tetrahedral group ‘2T’ is the group of 24 Hurwitz units under multiplication. This is the double cover of the rotations of the tetrahedron, which has order 12. There is a normal subgroup of order 8, which you may know as Q8.
• The binary octahedral group ‘2O’ is obtained by adjoining (1 + i)/sqrt(2) to the previous group, to get a group of 48 unit quaternions — the double cover of the rotations of a cube. They can be categorised as ‘even’ (if belonging to 2T) or ‘odd’ (otherwise), with the even elements forming a normal subgroup.
• The binary icosahedral group is the most interesting of all, containing the 120 unit icosians. It is not to be confused with C2 × A5 (the rotational and reflectional symmetries of a dodecahedron) or S5 (permutations of five objects), both of which also have order 120.

Electrons also have to rotate through 720° to return to their original orientations, so their orientations belong to Spin(3) rather than SO(3). An immediate consequence of this is that Hunter Spink can balance a beaker of water on the palm of his hand and rotate his arm through 720°, returning it to its original position.

SO(4) and Spin(4)

Let l and r be two quaternions of unit length. A mapping q → lqr* is a rotation in four-dimensional space; moreover, all rotations in SO(4) can be represented by such a pair of quaternions (l,r). Note also that (-l,-r) represents the same rotation, so we have the marvellous isomorphism Spin(3) × Spin(3) = Spin(4), which is really amazing.

We should be able to find double covers of the rotational symmetry groups of the Platonic hypersolids. We’ll start with the most unusual one, the 24-cell. Before we get to that, however, it is useful to consider a three-dimensional analogy:

The tetrahedron is self-dual, which means that a greater symmetry group can be obtained by composing it with its dual to form a stella octangula:

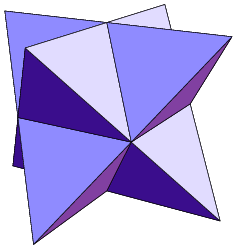
There is an analogy in four dimensions, where the 24-cell and its dual can be composed to yield an object with a rotational symmetry group of order 1152 instead of 576. The double cover of this, with order 2304, is obtained by choosing any ordered pair (l,r) of quaternions from the binary octahedral group 2O.

Recall that 2O has 2T as a normal subgroup, allowing us to refer meaningfully to ‘odd’ and ‘even’ rotations. If we add the additional constraint that l and r have the same parity, we get down to a group of order 1152, the double cover of the symmetry group of the 24-cell.

Going even further, note that 2O has Q8 as a normal subgroup of index 6, so we can define a homomorphism θ from 2O to the cyclic group C6, the kernel of which is Q8. Insisting further that θ(l) = θ(r), we get the rotations of the hypercube as a subgroup of the rotations of a 24-cell.

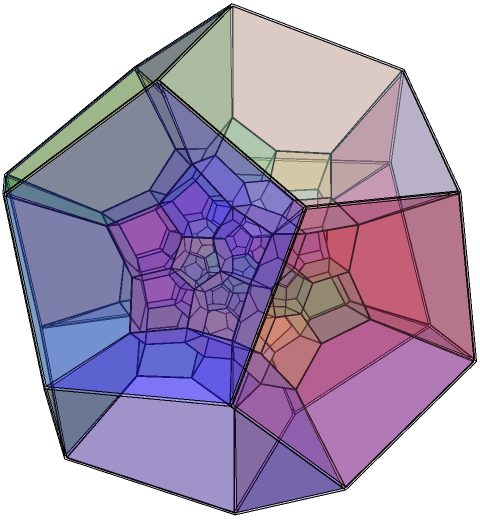
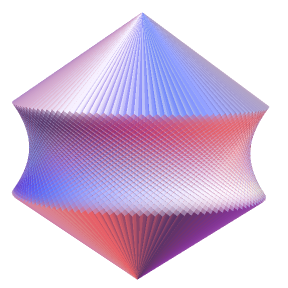
The 120-cell (pictured above using stereographic projection) has 7200 rotational symmetries. Its double cover corresponds exactly to 2I × 2I, i.e. the group of ordered pairs (l,r) of unit icosians. Some order-120 index-120 subgroup of this is the double cover of the rotational symmetry group of the 5-cell (four-dimensional simplex), isomorphic to 2I.

In even higher dimensions, Spin(6) is apparently isomorphic to SU(4), the ‘rotations’ of a ‘sphere’ in complex Euclidean 4-space.

So, what’s up with that, right…?

In case you haven’t heard of the field with one element, it’s a totally stupid non-existent thing that doesn’t exist. Nevertheless, its blatant non-existence did not deter several people from extensively investigating it, with the intention of proving the Riemann hypothesis. There’s quite an extensive Wikipedia entry about it, but the same applies to the Loch Ness Monster.

More interesting are elusive things which may or may not exist (not unlike many rumours involving me!). Let’s have a quick run-though of the various objects in this category:

• Wall-Sun-Sun primes: These are primes p for which p² is a divisor of the Fibonacci number F(p−l), where l is defined to be 1 if p = 5k ± 1 or −1 if p = 5k ± 2. If Fermat’s last theorem were false, there would exist examples of Wall-Sun-Sun primes. However, the converse is not true: we cannot conclude that there are no such primes, and it has been conjectured that infinitely many exist. A related notion is that of a Wieferich prime, where p² divides 2^(p-1)-1. Unlike Wall-Sun-Sun primes, we do have a couple of explicit examples, namely 1093 and 3511. If any larger Wieferich primes exist, they exceed 17 quadrillion.
• A 57-regular graph with diameter 2 and girth 5: A k-regular graph is a graph where every vertex is connected to k other vertices. If we insist that the diameter (maximum distance between any two vertices) is 2 and the girth (length of shortest cycle) is 5, then a theorem states that k must be either 2, 3, 7 or 57. We have examples for the first three cases (the pentagon, the Peterson graph and the Hoffman-Singleton graph, respectively), but no 57-regular graph with this property is known.
• Perfect cuboids: A 3-by-4 rectangle has a diagonal length of 5, which is also an integer. If all faces of a cuboid have this property, it is called an Euler brick (the smallest example is 240 by 117 by 44). A hypothetical Euler brick whose diameter is also an integer is called a perfect cuboid. No such examples are known.
• Connected aperiodic monotile: The two Penrose tiles together can tile the plane, but not in a periodic repeated pattern. Can a single tile have this property? Socolar and Taylor found a disconnected hexagonal example, but no connected example is known. A rough measure of ‘how close a tile is to being aperiodic’ is its isohedral number. The connected tile with the greatest isohedral number (10) was discovered by Joseph Myers and shown below.

The unique (up to similarity) known example of a 10-isohedral tile.

My calendar informs me that it will be Cipher Tuesday in a few days. I’ll make this one entirely textual, since I’ve had numerous complaints from a particular person about the impossibility of inputting images into his favourite cryptanalysis software.