Alexey Nigin has discovered a 15-face golyhedron, a vast improvement on my 32-face example. The optimisation was effected by the idea to only have a single club foot, and merely truncate the other end.
The smallest golyhedron therefore has either 11, 12 or 15 faces. Can you reduce Alexey’s upper bound even futher by finding an 11- or 12-faced golyhedron, or increase my lower bound by proving the impossibility thereof?
Make your own golyhedron
The faces of Alexey’s golyhedron can be orientation-preservingly juxtaposed into a 15-by-8 rectangle:
You can download and print an Alexeyhedron template to assemble your own model of the 15-face golyhedron. I bodged together an example from card and Sellotape; I’m sure that you could do better than this:

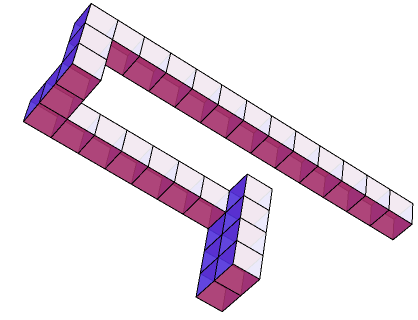


In your image of the Alexeyhedron, the arm connecting to the club foot should be one cube shorter.
I have found a 12-faced golyhedron!
http://yadi.sk/d/dmqoxL8kR6fSC
Wow!
I have just discovered an 11-faced golyhedron!
Here is its diagram:
1111111
15
15
A picture can be downloaded from https://yadi.sk/d/Zzw_Q6gKTZjwk.
Very optimal. Such minimality. So compact. Wow.
asics singspore sale
SPAM SPAM SPAM SPAM
What about a golyhedron that is more like a golygon? By that I mean it is defined by edges of consecutive integers (like a golygon), rather than square subfaces.