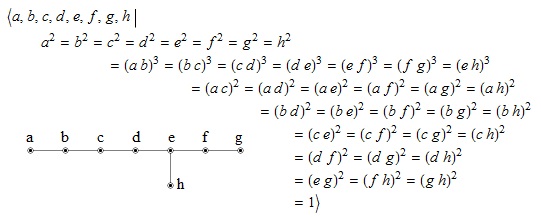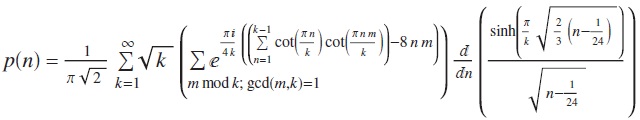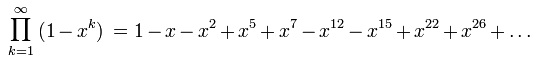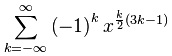Despite currently suffering from hay fever, I was able to combine the following attributes into a cipher:
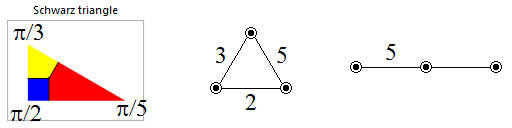
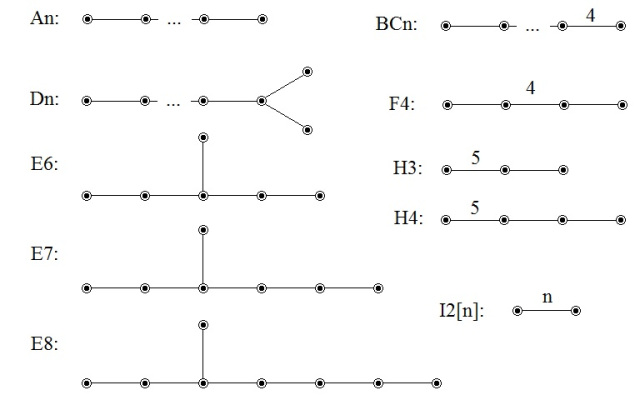
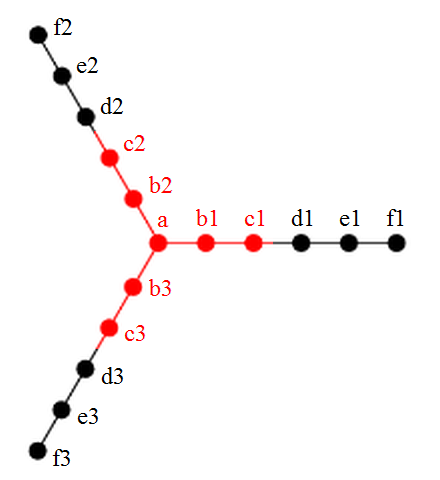
- The title is in alliterative Latin.
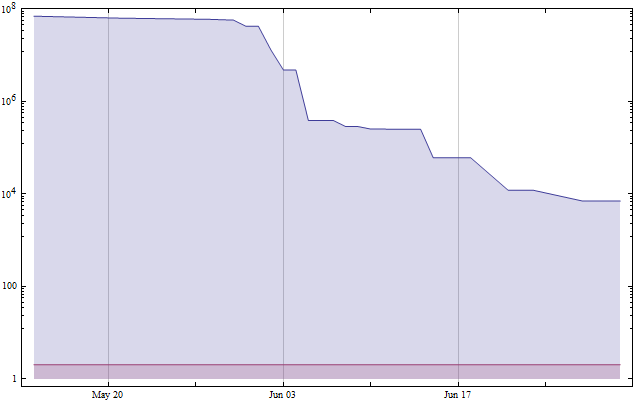
- The index of the cipher (36) is a perfect square, as is the length of the cipher text (784). Moreover, this is true even when one restrictively interprets ‘perfect square’ as ‘square of a perfect number’, in which case these are the first two perfect squares!
>++++[>++++<-]>[>++>+++>++++>+++++>++++++>+++++++<<<<<<- ]>>>+++.>>+++++++++++++++.-.-------.>++.<------.>++.+.<+ ++++++++++.-----------.>-.<++++++++.++++++.-.>-.<<<<<.>> >>--------.+++++++++.>-.<<<<<.>>>>-----------.+.--.+++++ +.>--.<-.---.>++.<++++.+++++.-------.<<<<.>>>>>++.<+.+.> -.<<<<<++++++++++++++.--------------.>>>++++.>-.---.<<<< .>>>>>---.<----.>+++..++++.<++++++++++++++.>-----.<----- ------.<<<<.>>>>+++++.>+.<<<<<.>>>>------.++++++++++++.> -.<-.---------.>.<<<<<++++++++++++++.--------------.>>++ +++++++.>>----.>++.<++++++++.+++++.<<<<.>>>>-----.>-.<<< <<.>>>>--.++++++++..-----------.<<<<.>>>>++.+++++++++.>- .<<<<<.>>>>.-------------.++++.>+++.--.<---.--.>+.<+++++ +++.+++++.-------.<<<<.>>>>>----.++.<++++++++.---------. -----.+++++++++++++.-----.>++.+++++.<<<<<++++++++++++++.
Enjoy.