This is now, at the time of writing, the longest article on cp4space.
We’ll begin with a very well-known problem, which asks whether it’s possible for three houses on the plane to be connected to three utility suppliers without crossings.
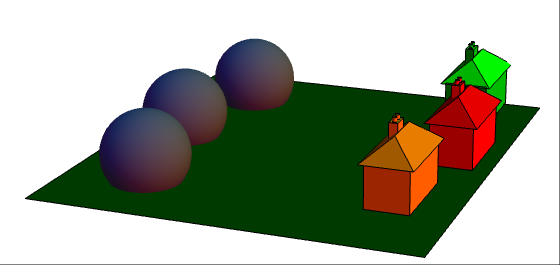
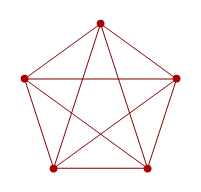
What appear to be three plutonium reactors are actually suppliers of electricity, water and gas, respectively. Ideally, we need to connect them with a planar arrangement of cables, aqueducts and pipes such that each of the three houses receive all three utilities. Proving that it’s impossible is not too difficult. Firstly, we reduce it to the graph-theoretic problem of trying to find a planar embedding of the complete bipartite graph K_3,3:
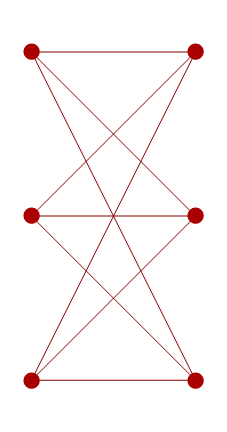
If we can find a planar embedding, all ‘faces’ created have an even number of edges, and therefore at least four edges. Plugging this inequality into Euler’s formula quickly leads to a contradiction, so there can be no such embedding. A related problem asks whether we can embed the complete graph K_5 into the plane; again, it is impossible by a similar argument. This problem might arise if you wanted to connect five houses in Edwin Abbott’s Flatland with telephone wires, long before the idea of a telephone exchange was invented.
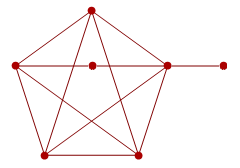
So, neither of these graphs are planar. Since K_5 is non-planar, the following graph doesn’t have a Tartarus-bound feline’s probability of being planar:
More generally, we obviously can’t make a graph less planar by performing any of the following operations:
- Contracting edges (replacing two adjacent vertices with a single vertex connected to all of their neighbours);
- Deleting edges (self-explanatory);
- Deleting vertices (for simplicity, isolated vertices).
If we can do this to a graph G to obtain another graph G’, then G’ is said to be a graph minor of G. There’s a very deep and powerful theorem, the Robertson-Seymour theorem, which states that graphs form something called a well-quasi-order under the relation of graph-minorship.
So, what is a well-quasi-order?
I’m sure I’ve mentioned the fact that there is no infinite decreasing sequence of ordinals. Since the ordinals have a total order imposed on them, that is equivalent to the fact that in any infinite sequence {x_1, x_2, x_3, …}, there must be elements x_i and x_j such that both i < j and x_i < x_j. A well-quasi-order has the exact same definition, applied to a partial order such as graph-minorship.
So, we can’t have an infinite sequence of graphs, such that no graph is a minor of a later graph. We’ll use this later. For now, let’s consider the set of non-planar (finite!) graphs. This is a nice, big, countably infinite set with the property that if a graph has a minor in this set, then it must itself inhabit the set. This set contains things like K_3,3, K_5 and that graph we made by augmenting K_5.
Obviously, there’s a lot of redundancy here. We can get rid of the augmented K_5, since it’s not giving us any more information (we already know that K_5 is non-planar, which implies that the augmented K_5 is also non-planar). If our set of ‘forbidden minors’ is infinite, then at least one graph must be a minor of another, and we can remove the larger graph. So, by induction, the minimal set of forbidden minors must be finite. Indeed, there’s a theorem called Wagner’s theorem which states that this minimal set has just two elements: K_5 and K_3,3.
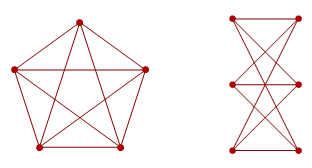
Any non-planar graph contains at least one of these as a minor. The best graph ever, the Petersen graph, actually features both of them as minors.
Linklessly embeddable graphs
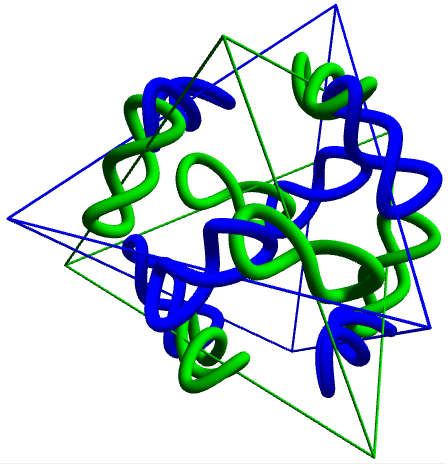
As well as planarity, we can consider other families of graphs closed under minorship. The Petersen graph is one of a set of seven forbidden minors for the property of linkless embedding. A graph is said to be linklessly embeddable if we can embed it into three-dimensional space such that no two cycles of vertices are linked. With the Petersen graph, we can’t. These seven forbidden minors include K_6 and are known collectively as the Petersen family (image courtesy of David Eppstein):

The light blue edges in the above graph of graphs represent Δ-Y transformations. These consist of replacing an induced 3-cycle with an induced star graph on 4 vertices, and are used for simplifying networks of resistors. The Petersen family shows that certain networks of resistors cannot be reduced by a suitable combination of Δ-Y transformations together with rules for resistances in series and parallel.
The set of graphs corresponding to reducible networks of resistors are closed under graph minorship, but the set of forbidden minors is far larger than the Petersen family. Yaming Yu demonstrated that this set contains at least 68 billion members.
Toroidal graphs
One way to ‘cheat’ at the water, gas and electricity problem is to place the houses and suppliers on the surface of a torus. Indeed, we can even have four houses and four utilities (e.g. water, gas, electricity and hydrogen) without any crossings. In particular, the graph K_4,4 is said to be toroidal. Similarly, the complete graph on seven vertices, K_7, is also toroidal (proof: seven-colour the hexagons in a honeycomb such that each hexagon is adjacent to hexagons of the six other colours, and such that the colouring is periodic in both dimensions). Whence, we obtain a brilliant polyhedron called the Szilassi polyhedron:

The Szilassi polyhedron has seven hexagonal faces, each of which neighbours the other six. We can convert this into the basic 7-couring of the hexagonal honeycomb by considering the universal cover of the Szilassi polyhedron. Informally, this is what we get when we unravel something to obtain a simply-connected space.
Even though we know that there is a finite set of forbidden minors for toroidal graphs, no-one has yet found one. This generalises to other surfaces as well as the plane and torus; examples include the Klein bottle, real projective plane and an infinitude of multi-holed tori.
Topological minors
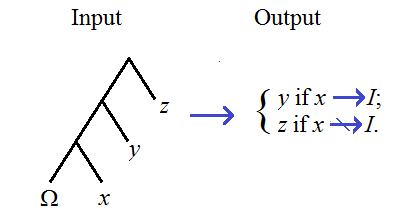
A related concept is that of a topological minor. All topological minors are graph minors, but not all graph minors are topological minors. A topological minor of a graph G is one which can be homeomorphically embedded into a subgraph of G by subdividing edges. I believe that an equivalent definition of topological minorship is to adapt the ordinary definition of graph minorship by replacing edge contractions with ‘double edge contractions’:
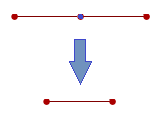
In the diagram above, the lilac vertex has degree 2. The red vertices have arbitrary degree, being possibly connected to vertices not shown in the diagram.
It transpires that Wagner’s theorem holds when ‘graph minor’ is replaced with ‘topological minor’ (the name for this modified theorem is Kuratowski’s theorem), but the Robertson-Seymour theorem does not hold in general. Nevertheless, it does apply to the special cases of trees (the result, Kruskal’s tree theorem, implies that TREE(3) exists) and to graphs where every vertex has degree at most 3 (since under this restriction, topological minors and graph minors are equivalent).
Friedman’s SSCG function
Let’s concentrate on simple subcubic graphs, that is to say each vertex has degree at most 3. Harvey Friedman formulated a fast-growing function, SSCG, which is defined like tree() but with subcubic graphs instead of trees. In particular, SSCG(k) is the length of the longest sequence of simple subcubic graphs, such that no graph is a minor of a later graph, and the nth graph has at most k + n vertices.
Friedman commented that SSCG(13) is much larger than TREE(3); here I’ll improve the bound to show that even SSCG(3) is larger than TREE(TREE(…TREE(3)…)) with a shedload of nested applications of the TREE function.
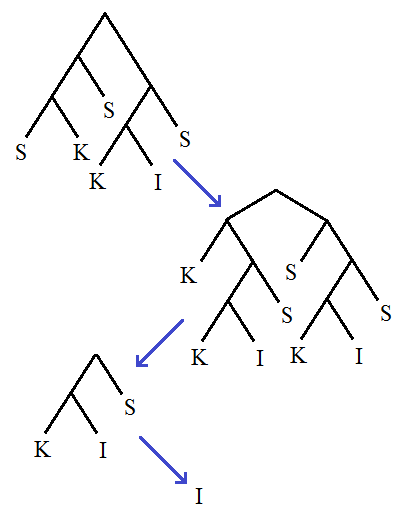
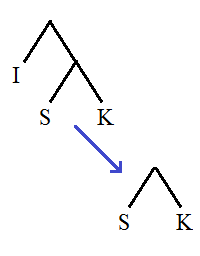
Note that there is no requirement that the graphs in question be connected. In the diagrams below, I’ll indicate the disjoint union of graphs with a plus (+) symbol, and the disjoint union of n identical graphs by preceding it with a number n. Firstly, the best lower bound I can attain for SSCG(2) is merely 3 × 2^(3 × 2^95) − 9 (i.e. less than a googolplex), which I conjecture is optimal.

It’s not difficult to show that the first few moves must be optimal. After the first move, we’re restricted to forests, and the second move further restricts us to disjoint unions of line graphs. I proceeded using a greedy algorithm, ensuring that the corresponding ordinal (replace each line graph on n vertices with the ordinal ω^(n−1)) is as large as possible. Greedy algorithms often give optimal solutions to simple problems, although others (travelling salesman, for example) resist this approach.
SSCG(2) is quite small. If we want to beat TREE(3), we’re going to need at least SSCG(3). We’ll also need some way of encoding labelled trees as simple subcubic graphs. Since the nodes of the tree can have arbitrary degree, but the vertices of the subcubic graph have degree ≤ 3, it is insufficient to use individual vertices to represent nodes. Instead, we encode each node as a fused cycle and triangle. The labels will be acyclic trees of vertices, for simplicity.
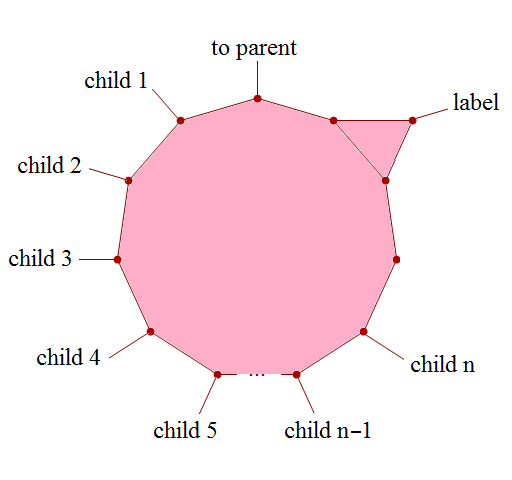
We connect these nodes together in the obvious way. For a tree to be a minor of another tree, it is obvious that nodes (pairs of connected cycles) must map to nodes, and that this corresponds to an inf- and label-preserving embedding. Actually, it is even more restrictive than that: the children must appear in the same order.
Each node has n + l + 6 vertices, where n is the number of children and l is the number of vertices in the label. We also need a distinguished ‘root’ node, designed so that it can only embed into the root of another tree. The root node is the only one where both cycles (triangles in this case) are eventually connected to other cycles.
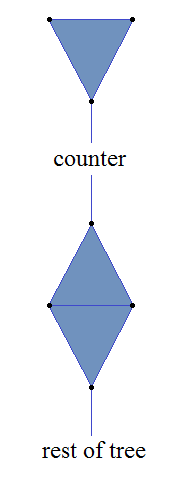
The root node doesn’t require a label. The size of the tree increases by up to l + 7 vertices for each step in the TREE sequence, so we need a ‘counter’ which decreases in length from l + 7 to 1 vertices between adjacent steps in the TREE sequence. This ensures that the nth graph doesn’t exceed its limit of n + k vertices.
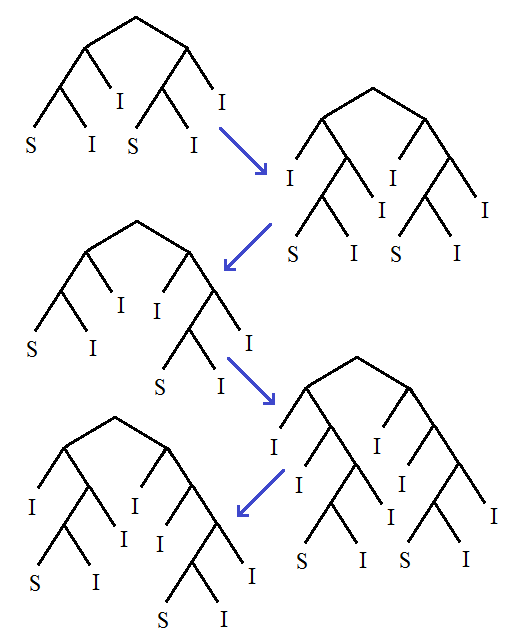
It’s easy to find a long sequence of graphs, which can take us up from 4 vertices to a large number of vertices, whilst not appearing as minors of any tree. Here’s how such a sequence might start:
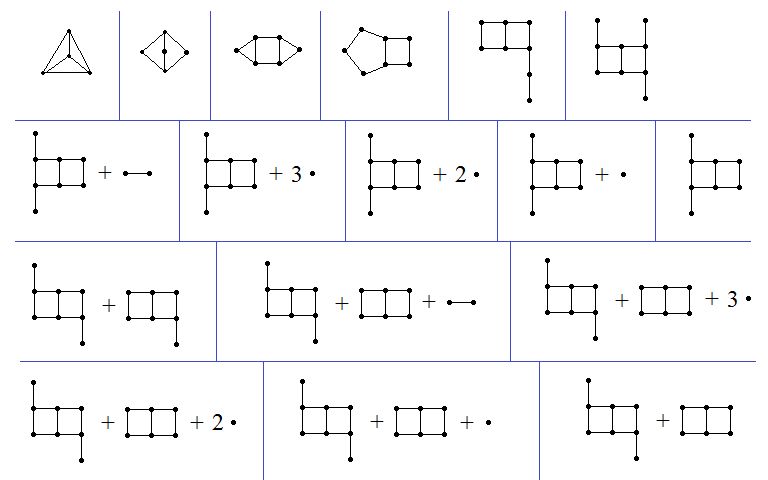
Note that the first two graphs are the forbidden minors for the set of outerplanar graphs (graphs which can be embedded on the plane so that all vertices are exposed). All subsequent graphs are outerplanar. The third graph has three fused cycles, and no subsequent graph has three fused cycles. All the following graphs contain a pair of fused 4-cycles, whereas the encodings of the labelled trees do not feature this as a minor.
After a while, subsequent graphs are a disjoint union of copies of the following ‘molecules’ together with the encoding of a labelled tree. The IUPAC identifiers for organic compounds are very useful for naming structures; James Aaronson and I designed a way of systematically naming polyominoes with a similar system.
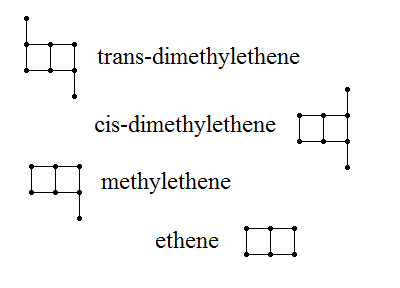
Note that none of these appear as a minor of a later molecule, nor as a minor of an encoding of a labelled tree. Hence, as I mentioned earlier, we can create an extremely long sequence of TREE(TREE(TREE(…TREE(3)…))) graphs, with an incredible number of nested applications of the TREE function. Consequently, we have the nice tight bounds SSCG(2) « TREE(3) « SSCG(3), where « indicates ‘mind-bogglingly greater than’.
Strength of the Robertson-Seymour theorem
I’m not sure whether anyone has located the ordinal which measures the strength of the Robertson-Seymour theorem. It’s obviously at least the small Veblen ordinal (since it implies Kruskal’s tree theorem, and SSCG overtakes TREE), and strictly below the Church-Kleene ordinal (deciding whether a graph is a minor of another graph is recursively decidable).
Anyhow, the proof of the Robertson-Seymour theorem is very difficult and occupies several hundred pages.